题目内容
2.扇形周长为1,当扇形的半径为R时,扇形有最大面积S,则R和S的值为( )| A. | $\frac{1}{4}$,$\frac{1}{16}$ | B. | $\frac{1}{2}$,$\frac{1}{8}$ | C. | $\frac{1}{4}$,$\frac{1}{8}$ | D. | $\frac{1}{2}$,$\frac{1}{16}$ |
分析 根据题意表示出扇形的弧长,根据扇形的面积公式列出代数式,利用配方法和偶次方的非负性解答即可.
解答 解:∵扇形周长为1,扇形的半径为R,
∴扇形的弧长为1-2R,
则S=$\frac{1}{2}$×(1-2R)×R=-R2+$\frac{1}{2}$R=-(R-$\frac{1}{4}$)2+$\frac{1}{16}$,
当R=$\frac{1}{4}$时,S的最大值为$\frac{1}{16}$,
故选:A.
点评 本题考查的是扇形面积的计算,配方法的应用,掌握扇形的面积公式是解题的关键.

练习册系列答案
相关题目
10.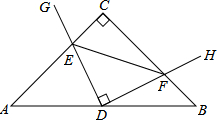 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
①AE+BF=$\frac{\sqrt{2}}{2}$AB,②△DEF始终为等腰直角三角形,
③S四边形CEDF=$\frac{1}{8}$AB2,
④AE2+CE2=2DF2.
其中正确的是( )
 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:①AE+BF=$\frac{\sqrt{2}}{2}$AB,②△DEF始终为等腰直角三角形,
③S四边形CEDF=$\frac{1}{8}$AB2,
④AE2+CE2=2DF2.
其中正确的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①④ | D. | ②③ |
11. 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )| A. | b | B. | -b | C. | -2a-b | D. | 2a-b |
 如图,在△ABC中,已知∠CAB=60°,AB∥CD.
如图,在△ABC中,已知∠CAB=60°,AB∥CD. 已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数.
已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数.