题目内容
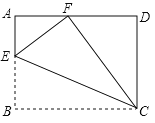
【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=3,BC=4,则tan∠AFE=__.
【答案】![]()
【解析】
由四边形ABCD是矩形,可得:∠A=∠B=∠D=90°,CD=AB=3,AD=BC=4,由折叠的性质可得:∠EFC=∠B=90°,CF=BC=4,由同角的余角相等,即可得∠DCF=∠AFE,然后在Rt△DCF中,即可求得答案.
解:∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,CD=AB=3,AD=BC=4,
由折叠的性质可得:∠EFC=∠B=90°,CF=BC=4,
∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,
∴∠DCF=∠AFE,
∵在Rt△DCF中,CF=4,CD=3,
∴DF=![]() ,
,
∴tan∠AFE=tan∠DCF=![]() =
=![]() ,
,
故答案为![]() .
.

【题目】某校在“校园体育文化节”活动中组织了“球类知识我知道”的竞赛活动,从初三年级1200名学生中随机抽查了100名学生的成绩(满分30分),整理得到如下的统计图表:
成绩(分) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
频率统计表
成绩分组 | 频数 | 频率 |
15≤x<18 | 3 | 0.03 |
18≤x<21 | a | 0.12 |
21≤x<24 | 20 | 0.20 |
24≤x<27 | 35 | 0.35 |
27≤x≤30 | 30 | b |
频数分布直方图
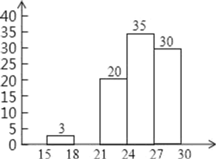
请根据所提供的信息解答下列问题:
(1)样本的众数是 分,中位数是 分;
(2)频率统计表中a= ,b= ;补全频数分布直方图;
(3)请根据抽样统计结果,估计该次竞赛中初三年级成绩不少于21分的大约有多少人?随机抽取一名同学的成绩,其值不小于24分的概率是多少?
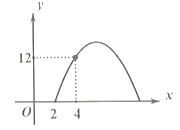
【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?