题目内容
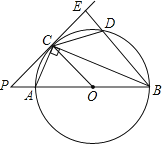
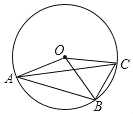
【题目】如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是( )个.
①AB=2BC;②![]() =2
=2![]() ;③∠ACB=2∠CAB;④∠ACB=∠BOC.
;③∠ACB=2∠CAB;④∠ACB=∠BOC.
A.1B.2C.3D.4
【答案】C
【解析】
首先取![]() 的中点D,连接AD,BD,由∠AOB=2∠BOC,易得
的中点D,连接AD,BD,由∠AOB=2∠BOC,易得![]() =2
=2![]() ,AD=BD=BC,继而证得AB<2BC,又由圆周角定理,可得∠AOB=4∠CAB,∠ACB=∠BOC=2∠CAB.
,AD=BD=BC,继而证得AB<2BC,又由圆周角定理,可得∠AOB=4∠CAB,∠ACB=∠BOC=2∠CAB.
解:取![]() 的中点D,连接AD,BD,
的中点D,连接AD,BD,
∵∠AOB=2∠BOC,
∴![]() =2
=2![]() ,故②正确,
,故②正确,
∴![]() =
=![]() =
=![]() ,
,
∴AD=BD=BC,
∵AB<AD+BD,
∴AB<2BC.故①错误,
∵∠AOB=2∠BOC,∠BOC=2∠CAB,
∴∠AOB=4∠CAB,
∵∠AOB=2∠ACB,
∴∠ACB=∠BOC=2∠CAB,故③④正确.
故选:C.


练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目