��Ŀ����
��2012•�ൺģ�⣩��ͼ���ڵ�������ABCD�У�AB=DC=5cm��AD=4cm��BC=10cm����E�ӵ�C��������1cm/s���ٶ���CB���B�ƶ�����F�ӵ�B������2cm/s���ٶ���BA�������A�ƶ�������F�����Aʱ����Eֹͣ�˶�������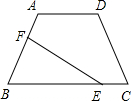 ����ʱ��Ϊt��s�� ��0��t��2.5�����ʣ�
����ʱ��Ϊt��s�� ��0��t��2.5�����ʣ�
��1����tΪ��ֵʱ��EFƽ�ֵ�������ABCD���ܳ���
��2������BFE�����ΪS��cm2������S��t�ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ�����AFECD��������BFE�����֮����3��2�����������t��ֵ���������ڣ�˵�����ɣ�
��4���ڵ�E��F�˶��Ĺ����У����߶�EF=
cm����ʱEF�ܷ�ֱƽ��AB��
 ����ʱ��Ϊt��s�� ��0��t��2.5�����ʣ�
����ʱ��Ϊt��s�� ��0��t��2.5�����ʣ���1����tΪ��ֵʱ��EFƽ�ֵ�������ABCD���ܳ���
��2������BFE�����ΪS��cm2������S��t�ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ�����AFECD��������BFE�����֮����3��2�����������t��ֵ���������ڣ�˵�����ɣ�
��4���ڵ�E��F�˶��Ĺ����У����߶�EF=
| 15 |
| 4 |
| 5 |
��������1��������֪�ó�BE+BF=
��AD+BC+CD+AB��=12������������ɣ�
��2����A��AN��BC��N����F��FG��BC��G�����AN�����ݡ�ABN�ס�FGB�ó�����ʽ�����FG�����������������ʽ������ɣ�
��3��������ڣ�������֪���������������������ó����̣�������ɣ�
��4��������ڣ�֤��ABN�ס�BEF���ó�����ʽ�����EF���ɣ�
| 1 |
| 2 |
��2����A��AN��BC��N����F��FG��BC��G�����AN�����ݡ�ABN�ס�FGB�ó�����ʽ�����FG�����������������ʽ������ɣ�
��3��������ڣ�������֪���������������������ó����̣�������ɣ�
��4��������ڣ�֤��ABN�ס�BEF���ó�����ʽ�����EF���ɣ�
����⣺��1����EFƽ�ֵ�������ABCD���ܳ���
��BE+BF=
��AD+BC+CD+AB��=12��
��10-t+2t=12��
t=2��
�𣺵�tΪ2sʱ��EFƽ�ֵ�������ABCD���ܳ���
��2��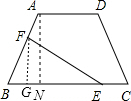
��A��AN��BC��N����F��FG��BC��G��
��BN=
��BC-AD��=
����10-4��=3��cm����
��AN��BC��FG��BC��
��FG��AN��
��ABN�ס�FGB��
��
=
��
��
=
��
FG=
t��
��S��BEF=
��BE��FG=
��10-t��•
t��
S=-
t2+8t��
��3���������ijһʱ��t��ʹ�����AFECD��������BFE�����֮����3��2��
S�����AFECD=S����ABCD-S��BFE=
����4+10����4-��-
t2+8t��=28+
t2-8t��
��2��28+
t2-8t��=3��-
t2+8t����
��ã�t=5+
������2.5����ȥ����t=5-
��
������ijһʱ��t��ʹ�����AFECD��������BFE�����֮����3��2��t��ֵ�ǣ�5-
��s��
��4���������EF��ֱƽ��AB��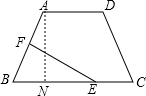
���ABN�ס�BEF��
=
��
=
��
EF=
��
��
���߶�EF=
cm����ʱEF���ܴ�ֱƽ��AB��
��BE+BF=
| 1 |
| 2 |
��10-t+2t=12��
t=2��
�𣺵�tΪ2sʱ��EFƽ�ֵ�������ABCD���ܳ���
��2��

��A��AN��BC��N����F��FG��BC��G��
��BN=
| 1 |
| 2 |
| 1 |
| 2 |
��AN��BC��FG��BC��
��FG��AN��
��ABN�ס�FGB��
��
| FG |
| AN |
| BF |
| AB |
��
| FG |
| 4 |
| 2t |
| 5 |
FG=
| 8 |
| 5 |
��S��BEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
S=-
| 4 |
| 5 |
��3���������ijһʱ��t��ʹ�����AFECD��������BFE�����֮����3��2��
S�����AFECD=S����ABCD-S��BFE=
| 1 |
| 2 |
| 4 |
| 5 |
| 4 |
| 5 |
��2��28+
| 4 |
| 5 |
| 4 |
| 5 |
��ã�t=5+
| 11 |
| 11 |
������ijһʱ��t��ʹ�����AFECD��������BFE�����֮����3��2��t��ֵ�ǣ�5-
| 11 |
��4���������EF��ֱƽ��AB��

���ABN�ס�BEF��
| EF |
| AN |
| DF |
| DN |
| EF |
| 4 |
5
| ||
| 3 |
EF=
| 10 |
| 3 |
| 15 |
| 4 |
| 5 |
���߶�EF=
| 15 |
| 4 |
| 5 |
���������⿼�������������ε��ж������ʣ����ε�����������ε���������ɶ�����֪ʶ���Ӧ�ã���Ҫ����ѧ����������ͽ�������������

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
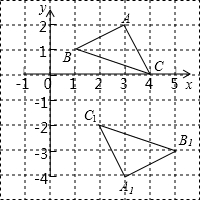 ��2012•�ൺģ�⣩��ͼ����ƽ��ֱ������ϵ�У�����ABC�Ƶ�E��ת180������A1B1C1��ȫ�غϣ����E�������ǣ�������
��2012•�ൺģ�⣩��ͼ����ƽ��ֱ������ϵ�У�����ABC�Ƶ�E��ת180������A1B1C1��ȫ�غϣ����E�������ǣ������� ��2012•�ൺģ�⣩��ͼ��һ��Ϊ2cm�Ŀ̶ȳ���Բ���ƶ������̶ȳߵ�һ����Բ����ʱ����һ����Բ�������㴦�Ķ���ǡ��Ϊ��2���͡�8������λ��cm�����Բ�İ뾶Ϊ��������
��2012•�ൺģ�⣩��ͼ��һ��Ϊ2cm�Ŀ̶ȳ���Բ���ƶ������̶ȳߵ�һ����Բ����ʱ����һ����Բ�������㴦�Ķ���ǡ��Ϊ��2���͡�8������λ��cm�����Բ�İ뾶Ϊ�������� ��2012•�ൺģ�⣩��ͼ����ABC�У���ACB=90�㣬�������ABC��BE���ۣ���Cǡ������AB���ϵĵ�D������AC=5cm����AE+DE��ֵΪ
��2012•�ൺģ�⣩��ͼ����ABC�У���ACB=90�㣬�������ABC��BE���ۣ���Cǡ������AB���ϵĵ�D������AC=5cm����AE+DE��ֵΪ