题目内容
（2012•青岛模拟）如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm）则该圆的半径为（ ）分析：设OB=rcm，由于刻度尺的宽为2cm，所以OC=r-2，再根据另一边与圆两个交点处的读数恰好为“2”和“8”可求出BC的长，在Rt△OBC中利用勾股定理即可得出r的值．
解答：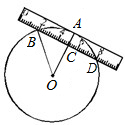
解：设OB=rcm，
∵刻度尺的宽为2cm，
∴OC=r-2，
∵另一边与圆两个交点处的读数恰好为“2”和“8”，
∴BC=
×BD=
×6=3，
在Rt△OBC中，
∵OB2=OC2+BC2，即r2=（r-2）2+32，解得r=
cm．
故选A．
解：设OB=rcm，∵刻度尺的宽为2cm，
∴OC=r-2，
∵另一边与圆两个交点处的读数恰好为“2”和“8”，
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OBC中，
∵OB2=OC2+BC2，即r2=（r-2）2+32，解得r=
| 13 |
| 4 |
故选A．
点评：本题考查的是垂径定理的应用及勾股定理，根据题意得出BC=3是解答此题的关键．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
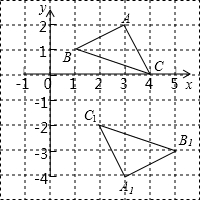（2012•青岛模拟）如图，在平面直角坐标系中，若△ABC绕点E旋转180°后与△A1B1C1完全重合，则点E的坐标是（ ）
（2012•青岛模拟）如图，△ABC中，∠ACB=90°，如果将∠ABC沿BE对折，点C恰好落在AB边上的点D处，若AC=5cm，则AE+DE的值为