题目内容
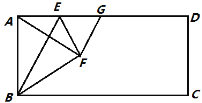
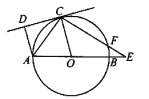
【题目】如图,已知:![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的切线,
的切线,![]() 于点
于点![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 平分
平分![]() .
.
(2)若![]() ,
,![]() .
.
①求![]() 的度数.
的度数.
②若![]() 的半径为
的半径为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)①∠OCE=45°;②2![]() -2.
-2.
【解析】
试题分析:(1)利用了切线的性质,平行线的判定和性质,等边对等角,角平分线的判定即可得证;(2)①根据(1)得出的AD//OC,从而得出同位角相等,再利用三角形的内角和定理即可求出答案;②作OG⊥CE于点G,可得FG=CG,根据等边对等角得出CG=OG=FG=2,在根据勾股定理得出GE,从而求出EF=GE-FG.
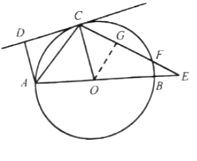
试题解析:(1)解:∵直线与⊙O相切,
∴OC⊥CD;
又∵AD⊥CD,
∴AD//OC,
∴∠DAC=∠OCA;
又∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC;
∴AC平分∠DAO.
(2)解:①∵AD//OC,∠DAO=105°,
∴∠EOC=∠DAO=105°;
∵∠E=30°,
∴∠OCE=45°.
②作OG⊥CE于点G,可得FG=CG,
∵OC=2![]() ,∠OCE=45°.
,∠OCE=45°.
∴CG=OG=2,
∴FG=2;
∵在RT△OGE中,∠E=30°,
∴GE=2![]() ,
,
∴EF=GE-FG=2![]() -2.
-2.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目