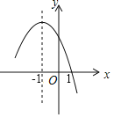题目内容
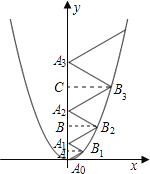
【题目】二次函数y=![]() x2的图象如图所示,点A0位于坐标原点,点A1、A
x2的图象如图所示,点A0位于坐标原点,点A1、A![]() 、A
、A![]() 、…、A
、…、A![]() 在y轴的正半轴上,点B
在y轴的正半轴上,点B![]() 、B
、B![]() 、B
、B![]() 、…、B
、…、B![]() 在二次函数y=
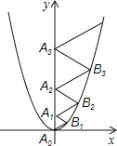
在二次函数y=![]() x2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A
x2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A![]() B
B![]() A
A![]() 的边长=____________.
的边长=____________.
【答案】2018
【解析】
分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,设A0A1=a,A1A2=b,A2A3=c,则AB1=![]() a,BB2=
a,BB2=![]() b,CB3=
b,CB3=![]() c,再根据所求正三角形的边长,分别表示B1,B2,B3的纵坐标,逐步代入抛物线y=
c,再根据所求正三角形的边长,分别表示B1,B2,B3的纵坐标,逐步代入抛物线y=![]() x2中,求a、b、c的值,得出规律.
x2中,求a、b、c的值,得出规律.
解:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
设A0A1=a,A1A2=b,A2A3=c,则AB1=![]() a,BB2=
a,BB2=![]() b,CB3=
b,CB3=![]() c,
c,
在正△A0B1A1中,B1(![]() a,
a,![]() ),
),
代入y=![]() x2中,得
x2中,得![]() =
=![]() ×
×![]() a2,解得a=1,即A0A1=1,
a2,解得a=1,即A0A1=1,
在正△A1B2A2中,B2(![]() b,1+
b,1+![]() ),
),
代入y=![]() x2中,得1+
x2中,得1+![]() =
=![]() ×
×![]() b2,解得b=2,即A1A2=2,
b2,解得b=2,即A1A2=2,
在正△A2B3A3中,B3(![]() c,3+
c,3+![]() ),
),
代入y=![]() x2中,得3+
x2中,得3+![]() =
=![]() ×
×![]() c2,解得c=3,即A2A3=3,
c2,解得c=3,即A2A3=3,
…
依此类推由此可得△A2017B2018A2018的边长=2018,
故答案为: 2018.

练习册系列答案
相关题目
【题目】我们把图1称为一个基本图形,显然这个基本图形中有6个矩形,将此基本图形不断复制并向上平移、叠加,这样得到图2,图3…(如图所示)
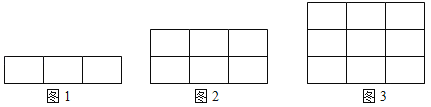
(1)观察图形,完成如表:
图形名称 | 矩形个数 |
图1 | 6 |
图2 | 18 |
图3 | 36 |
图4 | 60 |
图5 |
|
(2)根据以上规律猜想,图形n中共有多少个矩形(用含n的代数式表示)?