题目内容
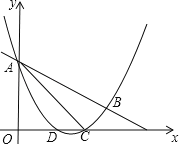
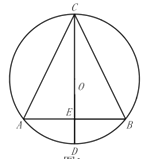
【题目】已知:![]() 内接于
内接于![]() ,直径
,直径![]() 交
交![]() 边于点
边于点![]() ,
,![]() .
.
(1)如图所示,求证:![]() ;
;
(2)如图所示,过点![]() 作
作![]() 于H,交
于H,交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
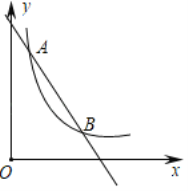
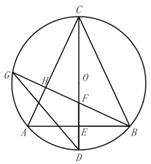
(3)如图所示,在(2)的条件下,延长![]() 至点
至点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
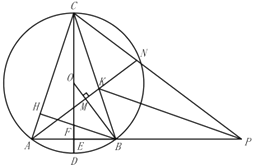
【答案】(1)证明见解析;(2)证明见解析;(3)5
【解析】
(1)通过证明△AEC≌△BEC,得到![]() ;
;
(2)连接DB,AG,由(1)知CD⊥AB,∠ACD=∠BCD,再根据等角的余角相等和同弧所对的圆周角相等可得到∠GBA=∠BGD,∠GAB=∠BDG,进而证明△DBG≌△AGB(AAS),即可得到GD=AB;
(3)根据AM⊥OB,结合前两问结论,易证![]() ,
,![]() ,再根据AAA证明△ABK∽△CBA,△CAB∽△PAC,设半径为r,则AC=
,再根据AAA证明△ABK∽△CBA,△CAB∽△PAC,设半径为r,则AC=![]() AE=
AE=![]() ,由
,由![]() 得
得![]() ,可求得
,可求得![]() ,则
,则![]() ,再由PN=AN=
,再由PN=AN=![]() ,则
,则![]() ,由
,由![]() ,可求得
,可求得![]() .
.
解:(1)证明:∵CD为直径,![]() ,
,
∴CD⊥AB,
∴∠AEC=∠BEC=90°,
在△AEC和△BEC中,
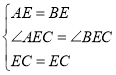 ,
,
∴△AEC≌△BEC,
∴![]() ;
;
(2)连接DB,AG,
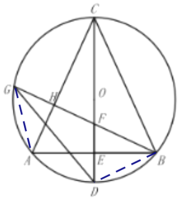
∵BG⊥AC,
∴∠HBA+∠HAB=90°,
由(1)知,CD⊥AB,∠ACD=∠BCD,
∴∠CAB+∠ACE=90°,
∴∠HBA=∠ACE,
∴∠GBA=∠BCD=∠BGD,
又∵∠GAB=∠BDG,
∴在△DBG和△AGB中,
 ,
,
∴△DBG≌△AGB(AAS),
∴GD=AB;
(3)连接BD,过点P作PQ⊥AN的延长线于N,
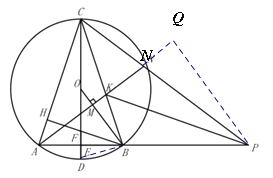
∵OD是![]() 的半径,AE=BE,
的半径,AE=BE,
∴OD⊥AB,
∵∠CFB为△CHF的外角,
∴∠CFB=∠CHF+∠HCF=90°+∠HCF,
∵∠CFB为△FEB的外角,
∴∠CFB=∠FEB+∠FBE=90°+∠FBE,
∴∠HCF=∠ABD,
∵∠HCF=∠ACD=∠ABD,
∴∠FBE=∠ABD,
∵∠BEF=∠BED,∠FBE=∠ABD,BE=BE,
∴△BFE≌△BDE,
∴FE=DE,
∵OF=AE,AE=BE,
∴OF=BE,
设FE=ED=a,OF=BE=b,
∴![]() ,
,
在Rt△OEB中,![]() ,
,
∴![]() ,
,
解得:![]() ,或
,或![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴∠KAB=∠EOB=2∠OCB=∠ACB,
而∠KBA=∠ABK,
∴△ABK∽△CBA,
∴∠KAB=∠ACB,
又∵AN=NP,
∴∠KAB=∠APN,
∴∠ACB=∠APN,
而∠CAB=∠PAC,
∴△CAB∽△PAC,
设半径为r,
则AC=![]() AE=
AE=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵PN=AN=![]() ,
,
则,![]() ,
,
∴![]() ,
,
得:![]() ,
,
∴![]() .
.