题目内容
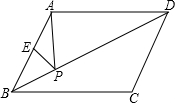
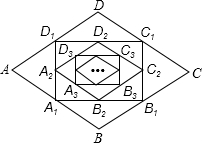 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2013B2013C2013D2013的面积是
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2013B2013C2013D2013的面积是25
| ||
| 22014 |
25
| ||
| 22014 |
分析:易得四边形A2B2C2D2的面积等于矩形A1B1C1D1的面积的
,同理可得四边形A3B3C3D3的面积等于四边形A2B2C2D2的面积
,那么等于矩形A1B1C1D1的面积的(
)2,同理可得所求四边形的面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
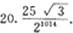 解:如图,连接AC、BD.则AC⊥BD.
解:如图,连接AC、BD.则AC⊥BD.
∵菱形ABCD中,边长为10,∠A=60°,
∴S菱形ABCD=
AC•BD=10×10×sin60°=50
.
∵顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1,
易证四边形A1B1C1D1 是矩形,
∴S矩形A1B1C1D1=
AC•
BD=
AC•BD=
S菱形ABCD.
同理,S四边形A2B2C2D2=
S矩形A1B1C1D1=(
)2S菱形ABCD,
S矩形A3B3C3D3=(
)3S菱形ABCD.
S矩形A2013B2013C2013D2013=(
)2013S菱形ABCD=
.
故答案为:
.

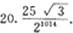 解:如图,连接AC、BD.则AC⊥BD.
解:如图,连接AC、BD.则AC⊥BD.∵菱形ABCD中,边长为10,∠A=60°,
∴S菱形ABCD=
| 1 |
| 2 |
| 3 |
∵顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1,
易证四边形A1B1C1D1 是矩形,
∴S矩形A1B1C1D1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
同理,S四边形A2B2C2D2=
| 1 |
| 2 |
| 1 |
| 2 |
S矩形A3B3C3D3=(
| 1 |
| 2 |
S矩形A2013B2013C2013D2013=(
| 1 |
| 2 |
25
| ||
| 22014 |
故答案为:
25
| ||
| 22014 |
点评:本题考查了中点四边形.找到中点四边形的面积与原四边形的面积之间的关系是解决本题的关键.

练习册系列答案
相关题目
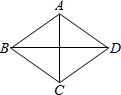 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.