Question

【题目】如图，以矩形OCPD的顶点O为原点，它的两条边所在的直线分别为x轴和y轴建立直角坐标系．以点P为圆心，PC为半径的⊙P与x轴的正半轴交于A、B两点．若抛物线y=ax2+bx+4经过A，B，C三点，且AB=6．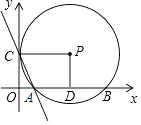

（1）求⊙P的半径R的长；
（2）求该抛物线的解析式；
（3）求出该抛物线与⊙P的第四个交点E的坐标．

Answer 1

【答案】
（1）解：如图1中，连接PA．

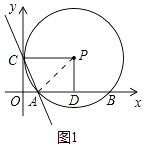
∵PD⊥AB，

∴AD=DB= AB=3，

∵抛物线y=ax2+bx+4与y轴交于点C，

∴C（0，4），

∴OC=4，

∵四边形PDOC是矩形，

∴PD=OC=3，∠PDA=90°，

∴PC=PA= = =5，

∴R=5

（2）解：由（1）可知A（，2，0），B（8，0），

把A、B两点坐标代入y=ax2+bx+4得到， ，

解得 ，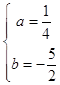

∴抛物线的解析式为y= x2﹣ x+4

（3）解：如图2中，

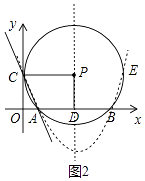
根据对称性，点C、点E关于对称轴x=5对称，

∵点C（0，4）

∴点E坐标（10，4）

【解析】（1）根据垂径定理可得AD=DB=3，在Rt△PAD中，根据PA= 即可解决问题．（2）先确定A、B两点坐标，再根据待定系数法即可解决问题．（3）根据对称性即可解决问题．