题目内容
【题目】已知抛物线C：y=x2﹣2x+1的顶点为P，与y轴的交点为Q，点F（1， 
）．
（1）求点P，Q的坐标；
（2）将抛物线C向上平移得到抛物线C′，点Q平移后的对应点为Q′，且FQ′=OQ′．
①求抛物线C′的解析式；
②若点P关于直线Q′F的对称点为K，射线FK与抛物线C′相交于点A，求点A的坐标．
【答案】
（1）
解：∵y=x2﹣2x+1=（x﹣1）2
∴顶点P（1，0），
∵当x=0时，y=1，
∴Q（0，1）
（2）
解：①设抛物线C′的解析式为y=x2﹣2x+m，
∴Q′（0，m）其中m＞1，
∴OQ′=m，
∵F（1， 
），
过F作FH⊥OQ′，如图：
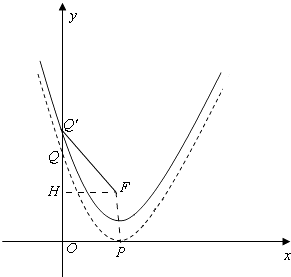
∴FH=1，Q′H=m﹣ ，
在Rt△FQ′H中，FQ′2=（m﹣ ）2+1=m2﹣m+ 
，
∵FQ′=OQ′，
∴m2﹣m+ =m2，
∴m= ，
∴抛物线C′的解析式为y=x2﹣2x+ ，
②设点A（x0，y0），则y0=x02﹣2x0+ ，
过点A作x轴的垂线，与直线Q′F相交于点N，则可设N（x0，n），
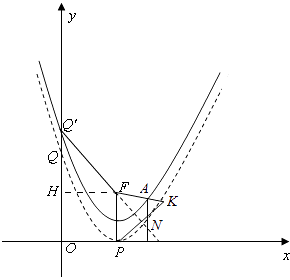
∴AN=y0﹣n，其中y0＞n，
连接FP，
∵F（1， ），P（1，0），
∴FP⊥x轴，
∴FP∥AN，
∴∠ANF=∠PFN，
连接PK，则直线Q′F是线段PK的垂直平分线，
∴FP=FK，有∠PFN=∠AFN，
∴∠ANF=∠AFN，则AF=AN，
根据勾股定理，得，AF2=（x0﹣1）2+（y0﹣ ）2，
∴（x0﹣1）2+（y0﹣ ）2=（x 
﹣2x0+ ）+y ﹣y0=y ，
∴AF=y0，
∴y0=y0﹣n，
∴n=0，
∴N（x0，0），
设直线Q′F的解析式为y=kx+b，
则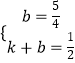 
，
解得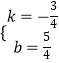 
，
∴y=﹣ 
x+ ，
由点N在直线Q′F上，得，0=﹣ x0+ ，
∴x0= 
，
将x0= 代入y0=x ﹣2x0+ ，
∴y0= 
，
∴A（ ， ）
【解析】此题是二次函数综合题，主要考查了待定系数法求解析式，线段的垂直平分线的判定和性质，解本题的关键是灵活运用勾股定理．（1）令x=0，求出抛物线与y轴的交点，抛物线解析式化为顶点式，求出点P坐标；（2）①设出Q′（0，m），表示出Q′H，根据FQ′=OQ′，用勾股定理建立方程求出m，即可．②根据AF=AN，用勾股定理，（x﹣1）2+（y﹣ ）2=（x2﹣2x+ ）+y2﹣y=y2 ， 求出AF=y，再求出直线Q′F的解析式，即可．
【考点精析】根据题目的已知条件，利用线段垂直平分线的判定的相关知识可以得到问题的答案，需要掌握和一条线段两个端点距离相等的点，在这条线段的垂直平分线上．
