题目内容
【题目】如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500 ![]() 米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
【答案】解:如图,过点A作AE⊥BC于点E,过点D作DF⊥AE于点F,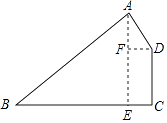
∵∠B=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,∠BAE=∠B=45°.
∵AB=500 ![]() 米,
米,
∴AE=BE=500 ![]() ×
× ![]() =500米.
=500米.
∵∠A=75°,
∴∠DAF=75°﹣45°=30°.
∵AD=200米,
∴DF= ![]() AD=100米,AF=200×
AD=100米,AF=200× ![]() =100
=100 ![]() 米.
米.
∵BC⊥CD,
∴四边形CDFE是矩形,
∴CD=EF=AE﹣AF=(500﹣100 ![]() )米,CE=DF=100米,
)米,CE=DF=100米,
∴AB+BC+AD+CD=500 ![]() +(500+100)+200+(500﹣100
+(500+100)+200+(500﹣100 ![]() )=(1300+500
)=(1300+500 ![]() ﹣100
﹣100 ![]() )米.
)米.
答:围墙的长度是(1300+500 ![]() ﹣100
﹣100 ![]() )米.
)米.
【解析】过点A作AE⊥BC于点E,过点D作DF⊥AE于点F,根据∠B=45°可得出△ABE是等腰直角三角形,故可得出AE=BE,∠BAE=∠B=45°.再由∠A=75°可得出∠DAF的度数,进而可得出AF及DF的长,根据BC⊥CD可得出四边形CDFE是矩形,故可得出CD=EF,CE=DF,据此可得出结论.

【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.