题目内容
【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
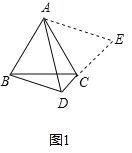
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)
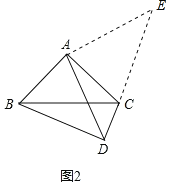
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

【答案】(1)DA=DB+DC;(2)![]() DA=DB+DC(或写成2DA2=(DB+DC)2),证明详见解析.
DA=DB+DC(或写成2DA2=(DB+DC)2),证明详见解析.
【解析】
(1)由等边三角形知AB=AC,∠BAC=60°,结合∠BDC=120°知∠ABD+∠ACD=180°,由∠ACE+∠ACD=180°知∠ABD=∠ACE,证△ABD≌△ACE得AD=AE,∠BAD=∠CAE,再证△ADE是等边三角形得DA=DE=DC+CE=DC+DB.
(2)延长DC到点E,使CE=BD,连接AE,先证△ABD≌△ACE得AD=AE,∠BAD=∠CAE,据此可得∠DAE=∠BAC=90°,由勾股定理知DA2+AE2=DE2,继而可得2DA2=(DB+DC)2.
解:(1)如图1,延长DC到点E,使CE=BD,连接AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BDC=120°,
∴∠ABD+∠ACD=180°,
又∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
∵∠ABC=60°,即∠BAD+∠DAC=60°,
∴∠DAC+∠CAE═60°,即∠DAE=60°,
∴△ADE是等边三角形,
∴DA=DE=DC+CE=DC+DB,即DA=DC+DB,
故答案为:DA=DC+DB;
(2)![]() DA=DB+DC(或写成2DA2=(DB+DC)2).
DA=DB+DC(或写成2DA2=(DB+DC)2).
延长DC到点E,使CE=BD,连接AE.
∵∠BAC=90°,∠BDC=90°,
∴∠ABD+∠ACD=180°.
∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE.
又∵AB=AC,CE=BD,
∴△ABD≌△ACE.
∴AD=AE,∠BAD=∠CAE.
∴∠DAE=∠BAC=90°.
∴DA2+AE2=DE2.
∴2DA2=(DB+DC)2.
∴![]() DA=DB+DC.
DA=DB+DC.