题目内容
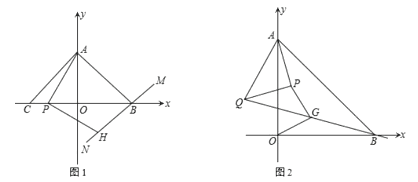
【题目】如图，A、B、C为⊙O上的点，PC过O点，交⊙O于D点，PD=OD，若OB⊥AC于E点． 
（1）判断A是否是PB的中点，并说明理由；
（2）若⊙O半径为8，试求BC的长．
【答案】
（1）解：A是PB的中点，
理由：连接AD，
∵CD是⊙O的直径，
∴AD⊥AC，
∵OB⊥AC，
∴AD∥OB，
∵PD=OD，
∴PA=AB，
∴A是PB的中点
（2）∵AD∥OB，
∴△APD∽△BPO，
∴ 
，
∵⊙O半径为8，
∴OB=8，
∴AD=4，
∴AC= 
=4 
，
∵OB⊥AC，
∴AE=CE=2 ，
∵OE= 
AD=2，
∴BE=6，
∴BC= 
=4 
．
【解析】（1）连接AD，由CD是⊙O的直径，得到AD⊥AC，推出AD∥OB，根据平行线等分线段定理得到PA=AB；（2）根据相似三角形的性质得到OB=8，求得AD=4，根据勾股定理得到AC= =4 ，根据垂径定理得到AE=CE=2 ，由勾股定理即可得到结论
【考点精析】掌握勾股定理的概念和垂径定理是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
练习册系列答案
相关题目
【题目】从2开始，连续的偶数相加，它们和的情况如表：
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
（1）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=；
（2）如下数表是由从1开始的连续自然数组成，观察规律：
①第n行的第一个数可用含n的式子表示为；
