题目内容
【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE
【答案】B
【解析】解:A、∵四边形ABCD是矩形,
∴AB=CD,∠A=∠B,
∵点P是BC的中点,
∴PB=PC,
在△APB和△DPC中, 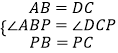 ,
,
∴△APB≌△DPC,
∴PA=PD,∠APB=∠DPC,
∵PD平分∠APC,
∴∠APD=∠CPD,
∴∠APB=∠APD=∠CPD,
∵∠APB+∠APD+∠CPD=180°,
∴∠APD=60°,
∵PA=PD,
∴△APD是等边三角形;
∴A正确,故A不符合题意;
C、∵PD⊥PE,
∴∠BPE+∠DPC=90°,∠APE+∠APD=90°,
∵∠APD=∠CPD,
∴∠APE=∠BPE,
∴ ![]() ,
,
∵AE=2BE,
∴ ![]() ,
,
在Rt△ABP中,sin∠BAP= ![]() ,
,
∴∠BAP=30°,
∴∠APB=60°,
∴∠BPE=∠APE=30°=∠BAP,
∴AE=PE,
∵EA⊥AD,EP⊥PD,
∴∠ADE=∠PDE,
在△ADE和△PDE中,  ,
,
∴△ADE≌△PDE,
∴∠AED=∠PED,
∵AE=PE,
∴DE⊥AP,
∴C正确,故C不符合题意;
D、∵△APD是等边三角形,
∴AP=DP,∠APD=60°,
∴∠CPD=60°,
∴∠APB=60°,
∴∠BPE=∠APE=∠PAB=30°
∴AE=PE
设BE=a,
在Rt△PBE中,BP= ![]() BE=
BE= ![]() a,PE=2a,
a,PE=2a,
∴AE=2a,
∴CD=AB=BE+AE=3a,
易证△APB≌△DPC,
∴PB=PC,
∴AD=BC=2BP=2 ![]() a,
a,
在Rt△ADE中,根据勾股定理,得,DE= ![]() =4a,
=4a,
∵BE+CD=a+3a=4a=DE,
∴D正确,故D不符合题意;
∴符合题意的只有B.
故选B.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为;






