题目内容
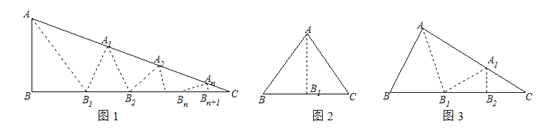
【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称 | 特征点的个数 |
图1 | 7 |
图2 | 12 |
… | … |
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.
【答案】(1)5n+2;(2)502;(3) 2017,理由见解析
【解析】整体分析:
(1)第一个图形可以看成是5×1+2=7个点,后面每一个图形比它前面的图形多5个点,由此即可得到规律;(2)由(1)中的规律进行计算;(3)根据(1)中的规律计算,注意n要是正整数.
解:(1)∵图1中有5×1+2=7个点,
图2中有5×2+2=12个点,
……
∴图n中有5n+2个特征点;
(2)当n=100时,5n+2=502,
即第100个图形的特征点有502个;
(3)由5n+2=2017得n=403,
即第403个图形有2017个特征点.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:

甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?