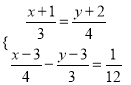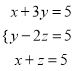题目内容
【题目】已知一张三角形纸片ABC（如图甲），其中AB=AC．将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD（如图乙）．再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF（如图丙）．原三角形纸片ABC中，∠ABC的大小为______°．
【答案】72
【解析】由题意得：∠ABC=2∠CBD，2∠BDC+∠ADE=180°，
∵AB=AC，∴∠ABC=∠C，
∵∠ADE=∠A，∠A+∠ABC+∠C=180°，
∴∠BDC=∠C=∠ABC，
∵∠CBD+∠C+∠BDC=180°，
∴∠CBD=∠A，
∴∠ABC=∠C=2∠A，
又∠A+∠ABC+∠C=180°，
∴∠A=36°，∴∠ABC=72°，
故答案为：72.
练习册系列答案
相关题目
【题目】我们把正六边形对角线的交点称为它的中心，正六边形的顶点及它的中心称作特征点，如图（1）有六个顶点和一个中心点，因此共有7个特征点，照图（1）的方式继续排列正六边形，使得相邻两个正六边形的一边重合，这样得到图（2），图（3）…
观察以上图形得到表：
图形的名称 | 特征点的个数 |
图1 | 7 |
图2 | 12 |
… | … |
（1）第n个图形的特征点有多少个？
（2）第100个图形的特征点有多少个？
（3）第几个图形有2017个特征点？请说明理由．
