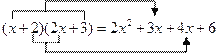题目内容
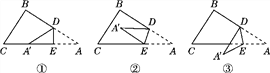
【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿△ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
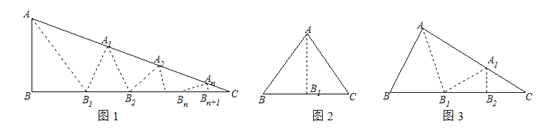
(1)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.
(2)根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 ;
(3)如果一个三角形的最小角是15°,且满足该三角形的三个角均是此三角形的好角,则此三角形另两个角的度数为 .
【答案】(1)∠B=3∠C;(2)∠B=n∠C;(3)15°,150°.
【解析】试题分析:(1)仔细分析题意根据折叠的性质及“好角”的定义即可作出判断;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的![]() 由
由![]() 又
又![]()
![]() 由此即可求得结果;
由此即可求得结果;
(3)因为最小角是15°是△ABC的好角,根据好角定义,则可设另两角分别为![]() (其中
(其中![]() 都是正整数),由题意得
都是正整数),由题意得![]() 所以
所以![]() 再根据
再根据![]() 都是正整数可得
都是正整数可得 ![]() 与
与![]() 是
是![]() 的整数因子,从而可以求得结果
的整数因子,从而可以求得结果
试题解析:(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是△ABC的好角;
理由如下:小丽展示的情形二中,
∵沿∠BAC的平分线![]() 折叠,
折叠,
∴![]()
又∵将余下部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与点C重合,
与点C重合,
∴![]()
∵![]() (外角定理),
(外角定理),
∴∠B=2∠C;
故答案是:是;
(2)∠B=3∠C;
在△ABC中,沿∠BAC的平分线![]() 折叠,剪掉重复部分;将余下部分沿
折叠,剪掉重复部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,将余下部分沿
折叠,剪掉重复部分,将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点C重合,则∠BAC是△ABC的好角.
与点C重合,则∠BAC是△ABC的好角.
证明如下:∵根据折叠的性质知, ![]()
∴根据三角形的外角定理知, ![]()
∵根据四边形的外角定理知, ![]()
根据三角形ABC的内角和定理知, ![]()
∴∠B=3∠C;
由小丽展示的情形一知,当∠B=∠C时,∠BAC是△ABC的好角;
由小丽展示的情形二知,当∠B=2∠C时,∠BAC是△ABC的好角;
由小丽展示的情形三知,当∠B=3∠C时,∠BAC是△ABC的好角;
故若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为∠B=n∠C;
故答案为:∠B=3∠C;∠B=n∠C
(3)由(2)知,∠B=n∠C,∠BAC是△ABC的好角,
因为最小角是![]() 是△ABC的好角,
是△ABC的好角,
根据好角定义,则可设另两角分别为![]() (其中m、n都是正整数).
(其中m、n都是正整数).
由题意,得![]() 所以m(n+1)=11
所以m(n+1)=11
因为m、n都是正整数,所以m与n+1是![]() 的整数因子,
的整数因子,
因此有: ![]()
所以m=1,n=10.
所以![]()
所以该三角形的另外两个角的度数分别为:15°,150°.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称 | 特征点的个数 |
图1 | 7 |
图2 | 12 |
… | … |
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.