题目内容
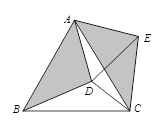
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.
,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.
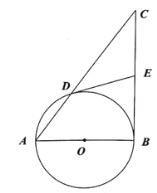
(1)求证:DE是![]() 的切线;
的切线;
(2)设![]() 的半径为r,证明
的半径为r,证明![]() ;
;
(3)若![]() ,求AD之长.
,求AD之长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由E为BC的中点,O为AB的中点,得到OE是△ABC的中位线,进而得到OE∥AC.再由平行线的性质及等腰三角形的性质可证∠1=∠2,即可得到△ODE≌△OBE,根据全等三角形对应角相等即可得到结论;
(2)证明△ADB∽△OBE,由相似三角形对应边成比例即可得到结论;
(3)根据切线长定理得到BE=DE=4.
由OE∥AC,得到∠4=∠C,则![]() ,解直角三角形OBE可得OB,OE的长,代入(2)中结论,即可得出AD的长.
,解直角三角形OBE可得OB,OE的长,代入(2)中结论,即可得出AD的长.
(1)∵AB⊥BC,∴∠OBC=90°.
∵E为BC的中点,O为AB的中点,
![]() ,
,
∴∠1=∠ODA,∠2=∠A.
∵OA=OD,∴∠A=∠ODA,∴∠1=∠2.
∵OD=OB,∠1=∠2,OE=OE,
∴△ODE≌△OBE,
∴∠ODE=∠OBE=90°,
∴DE为![]() 的切线;
的切线;
(2)∵∠2=∠A,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
因此,![]() ;
;
(3)∵DE、BE是⊙O的切线,∴BE=DE=4.
又∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
设OB=3x,则OE=5x,BE=4x.
∵BE=4,∴x=1,∴OB=3,OE=5.
又由(2)得:![]() ,
,
即:![]() ,
,
![]() .
.


练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目