题目内容
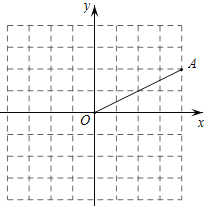
【题目】在平面直角坐标系xOy中,已知点A在抛物线y=x2+bx+c(b>0)上,且A(1,-1),
(1)若b-c=4,求b,c的值;
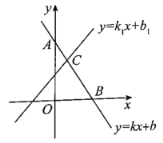
(2)若该抛物线与y轴交于点B,其对称轴与x轴交于点C,则命题“对于任意的一个k(0<k<1),都存在b,使得OC=k·OB.”是否正确?若正确,请证明;若不正确,请举反例;
(3)将该抛物线平移,平移后的抛物线仍经过(1,-1),点A的对应点A1为
(1-m,2b-1).当m≥-![]() 时,求平移后抛物线的顶点所能达到的最高点的坐标.
时,求平移后抛物线的顶点所能达到的最高点的坐标.
【答案】(1)b=1,c=-3;(2)对于任意的0<k<1,不一定存在b,使得OC=k·OB;(3)平移后抛物线的顶点所能达到的最高点坐标为(![]() ,-
,-![]() ).
).
【解析】
(1)把(1,-1)代入y=x2+bx+c得b+c=-2,与b-c=4构成方程组,解方程组即可求得;
(2)求得B(0,-2-b),C(-![]() ,0),即可求得OC=
,0),即可求得OC=![]() ,OB=2+b,根据题意当k=
,OB=2+b,根据题意当k=![]() 时,由OC=
时,由OC=![]() OB得
OB得![]() =
=![]() (2+b),此时b=-6<0不合题意,即可判定命题不正确;
(2+b),此时b=-6<0不合题意,即可判定命题不正确;
(3)把y=x2+bx+c化成顶点式,得到y=(x+![]() )2-
)2-![]() -2-b,根据平移的规律得到y=(x+
-2-b,根据平移的规律得到y=(x+![]() +m)2-
+m)2-![]() -2+b,把(1,-1)代入,进一步得到(1+
-2+b,把(1,-1)代入,进一步得到(1+![]() +m)2=(
+m)2=(![]() -1)2,即1+
-1)2,即1+![]() +m=±(
+m=±(![]() -1),分类求得m=-b,由m≥-
-1),分类求得m=-b,由m≥-![]() ,得到b≤
,得到b≤![]() ,即0<b≤
,即0<b≤![]() ,从而得到平移后的解析式为y=(x-
,从而得到平移后的解析式为y=(x-![]() )2-
)2-![]() -2+b,得到顶点为(
-2+b,得到顶点为(![]() ,-
,-![]() -2+b),设p=-
-2+b),设p=-![]() -2+b,即p=-
-2+b,即p=-![]() (b-2)2-1,即可得到p取最大值为-
(b-2)2-1,即可得到p取最大值为-![]() ,从而得到最高点的坐标.
,从而得到最高点的坐标.
(1)把(1,-1)代入y=x2+bx+c,可得b+c=-2,
解![]() ,可得b=1,c=-3,
,可得b=1,c=-3,
(2)不正确,
理由:由b+c=-2,得c=-2-b.
对于y=x2+bx+c,
当x=0时,y=c=-2-b.
抛物线的对称轴为直线x=-![]() .
.
所以B(0,-2-b),C(-![]() ,0).
,0).
因为b>0,
所以OC=![]() ,OB=2+b,
,OB=2+b,
当k=![]() 时,由OC=
时,由OC=![]() OB得
OB得![]() =
=![]() (2+b),此时b=-6<0不合题意.
(2+b),此时b=-6<0不合题意.
所以对于任意的0<k<1,不一定存在b,使得OC=kOB;
(3)由平移前的抛物线y=x2+bx+c,可得
y=(x+![]() )2-
)2-![]() +c,即y=(x+
+c,即y=(x+![]() )2-
)2-![]() -2-b.
-2-b.
因为平移后A(1,-1)的对应点为A1(1-m,2b-1)
可知,抛物线向左平移m个单位长度,向上平移2b个单位长度.
则平移后的抛物线解析式为y=(x+![]() +m)2-
+m)2-![]() -2-b+2b,
-2-b+2b,
即y=(x+![]() +m)2-
+m)2-![]() -2+b.
-2+b.
把(1,-1)代入,得
(1+![]() +m)2-
+m)2-![]() -2+b=-1.
-2+b=-1.
(1+![]() +m)2=
+m)2=![]() -b+1.
-b+1.
(1+![]() +m)2=(
+m)2=(![]() -1)2.
-1)2.
所以1+![]() +m=±(
+m=±(![]() -1).
-1).
当1+![]() +m=
+m=![]() -1时,m=-2(不合题意,舍去);
-1时,m=-2(不合题意,舍去);
当1+![]() +m=-(
+m=-(![]() -1)时,m=-b,
-1)时,m=-b,
因为m≥-![]() ,所以b≤
,所以b≤![]() .
.
所以0<b≤![]() ,
,
所以平移后的抛物线解析式为y=(x-![]() )2-
)2-![]() -2+b.
-2+b.
即顶点为(![]() ,-
,-![]() -2+b),
-2+b),
设p=-![]() -2+b,即p=-
-2+b,即p=-![]() (b-2)2-1.
(b-2)2-1.
因为-![]() <0,所以当b<2时,p随b的增大而增大.
<0,所以当b<2时,p随b的增大而增大.
因为0<b≤![]() ,
,
所以当b=![]() 时,p取最大值为-
时,p取最大值为-![]() ,
,
此时,平移后抛物线的顶点所能达到的最高点坐标为(![]() ,-
,-![]() ).
).

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
每件T恤的利润(元) | 销售量(件) | |
第一个月 | ||
清仓时 |
(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?