Question

【题目】如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、S4．则S1+S2+S3+S4等于（ ）

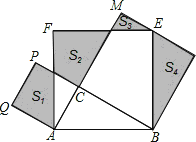
A．14 B．16 C．18 D．20

Answer 1

【答案】C．

【解析】

试题分析：如图：

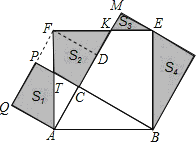
图中S4=SRt△ABC．S3=S△FPT，

∴S1+S3=SRt△ABC．

S2的左上方的顶点为F，过F作AM的垂线交AM于D，可证明Rt△ADF≌Rt△ABC，而图中Rt△DFK全等于①，

所以S2=SRt△ABC．

S1+S2+S3+S4

=（S1+S3）+S2+S4

=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积

=Rt△ABC的面积×3

=4×3÷2×3

=18．

故选C．