题目内容
【题目】如图所示,在平面直角坐标系xoy中,抛物线y=(m﹣1)x2﹣(3m﹣4)x﹣3与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴是经过(1,0)且与y轴平行的直线,点P是抛物线上的一点,点Q是y轴上一点;
(1)求抛物线的函数关系式;
(2)若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)若tan∠PCB= ![]() ,求点P的坐标.
,求点P的坐标.
【答案】
(1)
解:当y=0时,(m﹣1)x2﹣(3m﹣4)x﹣3=0,
解得x1= ![]() ,x2=3,即A(
,x2=3,即A( ![]() ,0)B(3,0),
,0)B(3,0),
由A,B关于x=1对称,得
![]() =﹣1,解得m=2,
=﹣1,解得m=2,
即A(﹣1,0),
函数解析式为y=x2﹣2x﹣3;
(2)
解:由四边形ABPQ是平行四边形,得
PQ∥AB,PQ=AB=4,
当PQ=4,即x=4时,y=5,即P(4,5);
当x=﹣4时,y=21,即P(﹣4,21),
综上所述:四边形ABPQ是平行四边形P(4,5),(﹣4,21);
(3)
解:如图
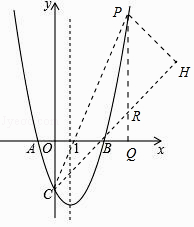 ,
,
过P作PQ⊥x轴于Q,交CB延长线于R,过P作PH⊥BC于H,
设P(m,m2﹣2m﹣3),
∵抛物线y=x2﹣4x+3与坐标轴交于A,B,C三点,
∴x=0,则y=﹣3;
y=0,则0=x2﹣4x+3,
解得:x1=﹣1,x2=3,
故A(﹣1,0),B(3,0),C(0,﹣3),
设直线BC的解析式为:y=kx+b,
则 ![]() ,
,
解得: ![]() ,
,
故直线BC解析式:y=x﹣3,
∴R(m,m﹣3),PR=m2﹣2m﹣3﹣(m﹣3)=m2﹣3m,
∵OB=OC=3,
∴∠CBQ=135°,
∴∠HPR=45°,
∵CO=OB,
∴∠OCR=45°,
∴CR= ![]() OQ=
OQ= ![]() m,
m,
∴PH=RH=PR÷ ![]() =
= ![]() m(m﹣3),
m(m﹣3),
又CR= ![]() OQ=
OQ= ![]() m,
m,
∴CH= ![]() m+
m+ ![]() m(m﹣3)
m(m﹣3)
= ![]() m(m+1)
m(m+1)
由tan∠PCB= ![]() =
= ![]() =
= ![]() ,
,
解得:m=7,
则m2﹣2m﹣3=32,
故P(7,32).
【解析】(1)根据自变量与函数值得对应关系,可得关于x的方程,根据解方程,可得A,B点坐标,根据函数值相等的点关于对称轴对称,可得m的值;(2)根据平行四边形的对边平行且相等,可得PQ的长,根据解方程,可得P点的横坐标,根据自变量与函数值得对应关系,可得答案;(3)根据题意首先得出直线BC的解析式,进而利用PR的长结合tan∠PCB=2得出P点横坐标,进而求出答案.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.