题目内容
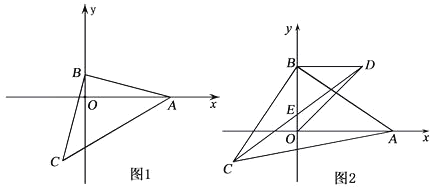
【题目】已知：点 A(4，0)，点 B 是 y 轴正半轴上一点，如图 1，以 AB 为直角边作等腰直角三角形 ABC ABC 90．
（1）若 AC 6，求点B 的坐标；
（2）当点B 坐标为(0，1)时，求点C 的坐标；
（3）如图 2，以 OB 为直角边作等腰直角△OBD，点D在第一象限，连接CD交 y 轴于点E．在点 B 运动的过程中，BE 的长是否发生变化？若不变，求出 BE 的长；若变化，请说明理由．
【答案】（1）（0，
） （2）（-1，-3） （3）BE长保持不变，BE的长为2
【解析】
（1）根据AC的长求出AB的长，再用勾股定理求B点坐标.
（2）过C作CM⊥y轴于M，通过判定△BCM≌△ABO（AAS），得出CM=BO=1，BM=AO=4，进而得到OM=3，据此可得C（-1，-3）；
（3）过C作CM⊥y轴于M，根据△BCM≌△ABO，可得CM=BO，BM=OA=4，再判定△DBE≌△CME（AAS），可得BE=EM，进而得到BE=
BM=2．
（1）∵△ABC是等腰直角三角形，AC 6
∴2AB2=36
∴AB=
设B点坐标为（0，a）(a>0)
在直角三角形AOB中，A(4，0)
∴16+a2=18
∴a=
∴B点的坐标为（0，）
（2）如图1，过C作CM⊥y轴于M．
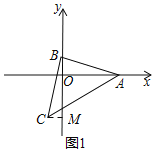
∵CM⊥y轴，
∴∠BMC=∠AOB=90°，
∴∠ABO+∠BAO=90°
∵∠ABC=90°，
∴∠CBM+∠ABO=90°，
∴∠CBM=∠BAO，
在△BCM与△ABO中，
，
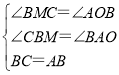∴△BCM≌△ABO（AAS），
∴CM=BO=1，BM=AO=4，
∴OM=3，
∴C（-1，-3）；
（3）在B点运动过程中，BE长保持不变，BE的长为2，
理由：如图2，过C作CM⊥y轴于M，
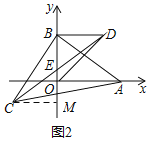
由（1）可知：△BCM≌△ABO，
∴CM=BO，BM=OA=4．
∵△BDO是等腰直角三角形，
∴BO=BD，∠DBO=90°，
∴CM=BD，∠DBE=∠CME=90°，
在△DBE与△CME中，
，
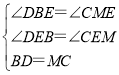∴△DBE≌△CME（AAS），
∴BE=EM，
∴BE=BM=2．
