Question

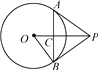
【题目】如图，直尺、三角尺都和⊙O相切，B是切点，且AB＝8 cm.求⊙O的直径．

Answer 1

【答案】16

【解析】连接OE、OA、OB，根据切线长定理和切线性质求出∠OBA=90°，∠OAE=∠OAB=∠BAC，求出∠BAC，求出∠OAB和∠BOA，求出OA，根据勾股定理求出OB即可．

设三角尺与⊙O相切于点E，三角尺斜边所在直线为AC，连结OE，OA，OB.

∵AC，AB都是⊙O的切线，切点分别是E，B， ∴∠OBA＝∠OEA＝90°.

又∵OB＝OE，OA＝OA，∴Rt△OBA≌Rt△OEA， ∴∠OAB＝∠OAE＝∠BAC.

∵∠CAD＝60°，∴∠BAC＝120°， ∴∠OAB＝×120°＝60°，∴∠BOA＝30°，

∴OA＝2AB＝16(cm)． 由勾股定理，得OB＝ ＝＝8 (cm)，

即⊙O的半径是8 cm， ∴⊙O的直径是16 cm.