题目内容
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想; 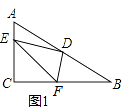
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明) 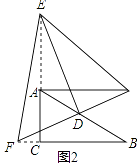
【答案】
(1)结论:AE2+BF2=EF2.
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.
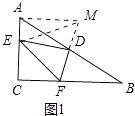
在△ADM和△BDF中,
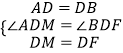 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2,
∴AE2+BF2=EF2.
(2)如图2中,结论不变.AE2+BF2=EF2
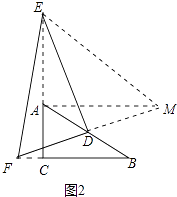
理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
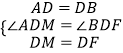 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2,
∴AE2+BF2=EF2.
【解析】(1)结论:AE2+BF2=EF2 . 如图1中,延长FD到M,使得DM=DF,连接AM,EM.首先证明△ADM≌△BDF,得到AM=FB,再证明△AEM是直角三角形,理由勾股定理即可解决问题.(2)结论不变,证明方法类似.
【考点精析】关于本题考查的直角三角形斜边上的中线,需要了解直角三角形斜边上的中线等于斜边的一半才能得出正确答案.

练习册系列答案
相关题目