Question

【题目】如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x袖于点M ， 交y轴于点N ， 再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P ． 若点P的坐标为（2a ， b+1），则a与b的数量关系为（　　）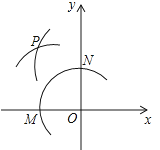
A.a-b
B.2a+b=-1
C.2a-b=l
D.2a+b=l

Answer 1

【答案】B
【解析】 根据作图方法可得点P在第二象限角平分线上，
则P点横纵坐标的和为0，
故2a+b+1=0，
整理得：2a+b=-1
选：B．
根据作图过程可得P在第二象限角平分线上，由角平分线的性质：角的平分线上的点到角的两边的距离相等可得|2a|=|b+1|，再根据P点所在象限可得横纵坐标的和为0，进而得到a与b的数量关系