题目内容
【题目】若∠C=α,∠EAC+∠FBC=β 
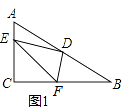
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
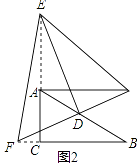
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是 . (用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1 , ∠EAP1与∠FBP1的平分线交于P2;依此类推,则∠P5= . (用α、β表示)
【答案】
(1)解:∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠MAC+∠NCB= ![]() ∠EAC+
∠EAC+ ![]() ∠FBC=
∠FBC= ![]() β,
β,
∵AM∥BN,
∴∠C=∠MAC+∠NCB,
即α= ![]() β;
β;
(2)α=∠APB+ ![]() β或α+∠APB=
β或α+∠APB= ![]() β
β
(3)α﹣ ![]() β
β
【解析】(2)∵∠EAC的平分线与∠FBC平分线相交于P, ∴∠PAC+∠PBC= ![]() ∠EAC+
∠EAC+ ![]() ∠FBC=
∠FBC= ![]() β,
β,
若点P在点C的下方,则∠C=∠APB+(∠PAC+∠PBC),
即α=∠APB+ ![]() β,
β,
若点P在点C的上方,则∠C+∠APB=∠PAC+∠PBC,
即α+∠APB= ![]() β;
β;
综上所述,α=∠APB+ ![]() β或α+∠APB=
β或α+∠APB= ![]() β;
β;
3)由(2)得,∠P1=∠C﹣(∠PAC+∠PBC)=α﹣ ![]() β,
β,
∠P2=∠P1﹣(∠P2AP1+∠P2BP1),
=α﹣ ![]() β﹣
β﹣ ![]() β=α﹣
β=α﹣ ![]() β,
β,
∠P3=α﹣ ![]() β﹣
β﹣ ![]() β=α﹣
β=α﹣ ![]() β,
β,
∠P4=α﹣ ![]() β﹣
β﹣ ![]() β=α﹣
β=α﹣ ![]() β,
β,
∠P5=α﹣ ![]() β﹣
β﹣ ![]() β=α﹣
β=α﹣ ![]() β.
β.
所以答案是:(2)α=∠APB+ ![]() β或α+∠APB=
β或α+∠APB= ![]() β;(3)α﹣
β;(3)α﹣ ![]() β.
β.
【考点精析】根据题目的已知条件,利用平行线的性质和三角形的内角和外角的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案