题目内容
【题目】平面上5个圆最多能把平面分成多少个部分?一般地,n个圆最多能把平面分成多少个部分?
【答案】5个圆最多将平面分成22个部分,n个圆最多分平面为n2﹣n+2.
【解析】
根据题意,探索出圆的个数与分成的平面个数的关系,从而得出结论.
1个圆最多能把平面分成2个部分,
2个圆最多能把平面分成4个部分;
3个圆最多能把平面分成8个部分;
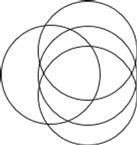
现在加入第4个圆,为了使分成的部分最多,第4个圆必须与前面3个圆都有两个交点,
如图所示,因此得6个交点将第4个圆的圆周分成6段圆弧,而每一段圆弧将原来的部分一分为二,即增加了一个部分,于是4个圆最多将平面分成8+6=14个部分,
同理,5个圆最多将平面分成14+8=22个部分,
一般地,n个圆最多分平面为:
2+1×2+2×2+…+(n﹣1)×2,
=2+2[1+2+…+(n﹣1)],
=n2﹣n+2.

练习册系列答案
相关题目