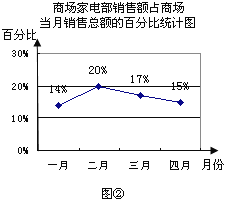
题目内容
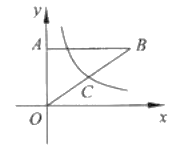
【题目】如图,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在第一象限,函数
在第一象限,函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,并且点
,并且点![]() 为边
为边![]() 的中点.若
的中点.若![]() 的面积为12,则
的面积为12,则![]() 的值为______.
的值为______.
【答案】6
【解析】
过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,由此可知![]() ODC∽
ODC∽![]() OEB,CD∥BE,结合
OEB,CD∥BE,结合![]() AOB为直角三角形可得出四边形OEBA为矩形,从而得出“BE=AO,AB=OE”,再由点C为线段OB的中点,即可得出“BE=2CD,OE=2OD”,结合三角形的面积公式以及反比例函数系数k的几何意义即可得出|k|=6,结合反比例函数在第一象限内有图象即可得出结论.
AOB为直角三角形可得出四边形OEBA为矩形,从而得出“BE=AO,AB=OE”,再由点C为线段OB的中点,即可得出“BE=2CD,OE=2OD”,结合三角形的面积公式以及反比例函数系数k的几何意义即可得出|k|=6,结合反比例函数在第一象限内有图象即可得出结论.
解:过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,如图所示.
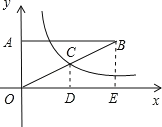
∵CD⊥x轴,BE⊥x轴,
∴![]() ODC∽
ODC∽![]() OEB,CD∥BE.
OEB,CD∥BE.
∵![]() AOB为直角三角形,
AOB为直角三角形,
∴∠OAB=90°=∠AOE,
∴AB∥OE,
∴四边形OEBA为矩形,
∴BE=AO,AB=OE.
又∵点C为线段OB的中点,
∴BE=2CD,OE=2OD.
∵S△AOB=![]() AOAB
AOAB
=![]() BEOE
BEOE
=![]() (2CD)(2OD)
(2CD)(2OD)
=4S△OCD
=12,
∴S△OCD=3=![]() |k|,
|k|,
解得:|k|=6.
∵反比例函数图象有一部分在第一象限内,
∴k=6.
故答案为:6.

练习册系列答案
相关题目