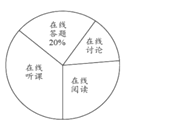
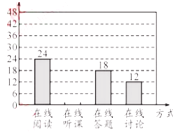
��Ŀ����
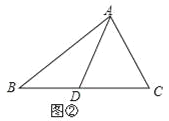
����Ŀ��(1)��ͼ�٣�AD�ǡ�ABC�����ߣ���ABD���ACD�������������������ϵ��Ϊʲô��
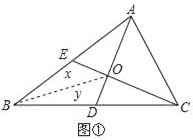
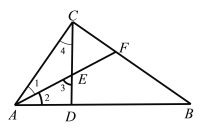
(2)�������ε������ΪS�����磺��ABC�������ΪS��ABC����ͼ�ڣ���֪S��ABC��1����ABC������AD��CE�ཻ�ڵ�O�����ı���BDOE�������
С������(1)�Ľ��ۣ�������������⣬�ⷨ���£�
����BO����S��BEO��x��S��BDO��y����(1)���ۿɵã�S��BCE��S��BAD��![]() S��ABC��
S��ABC��![]() ��S��BCO��2S��BDO��2y��S��BAO��2S��BEO��2x������
��S��BCO��2S��BDO��2y��S��BAO��2S��BEO��2x������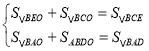 ��
��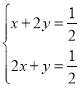 ����x��y��
����x��y��![]() �����ı���BDOE���Ϊ
�����ı���BDOE���Ϊ![]() ��
��
���������ķ���������������⣺
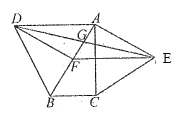
����ͼ�ۣ���֪S��ABC��1��D��E��BC���ϵ����ȷֵ㣬F��G��AB���ϵ����ȷֵ㣬AD��CF���ڵ�O�����ı���BDOF�������
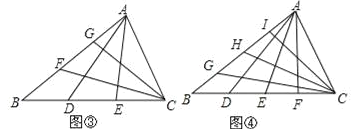
����ͼ�ܣ���֪S��ABC��1��D��E��F��BC���ϵ��ĵȷֵ㣬G��H��I��AB���ϵ��ĵȷֵ㣬AD��CG���ڵ�O�����ı���BDOG�����Ϊ ��
���𰸡���1��S��ABD=S��ACD����2����![]() ����
����![]()
��������
��1�����õȵȸߵ���������������⼴�ɣ�
��2��������BO����S��BDO=x��S��BGO=y�����������μ�������ϵ�г���������⼴�ɣ�
������BO����S��BDO=x��S��BGO=y�����������μ�������ϵ�г���������⼴�ɣ�
�⣺��1��S��ABD=S��ACD��
��AD�ǡ�ABC�����ߣ�
��BD=CD��
�֡ߡ�ABD���ACD����ȣ�
��S��ABD=S��ACD��
��2������ͼ3������BO����S��BFO=x��S��BDO=y��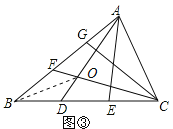
S��BCF=S��ABD=![]() S��ABC=
S��ABC=![]()
S��BCO=3S��BDO=3y��
S��BAO=3S��BFO=3x��
����![]() ����
����
����x+y=![]() �����ı���BDOF�����Ϊ
�����ı���BDOF�����Ϊ![]() ��
��
����ͼ������BO����S��BDO=x��S��BGO=y��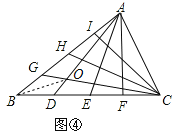
S��BCG=S��ABD=![]() S��ABC=
S��ABC=![]() ��
��
S��BCO=4S��BDO=4x��
S��BAO=4S��BGO=4y��
����![]() ����
����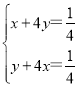
����x+y=![]() �����ı���BDOG�����Ϊ
�����ı���BDOG�����Ϊ![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�