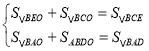Question

【题目】已知正方形ABCD的边长为6，E、F、P分别是AB、CD、AD上的点（均不与正方形顶点重合）且PE=PF,PE⊥PF.

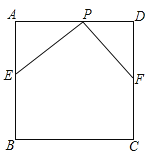
（1）求证：AE+DF=6

（2）设AE=，五边形EBCFP的面积为，求与的函数关系式，并求出的取值范围.

Answer 1

【答案】（1）证明见解析；

（2）y＝x26x＋36，y的取值范围是27≤y＜36．

【解析】

（1）根据∠A＝∠D＝∠EPF＝90°和PE＝PF的条件，易证△AEP与△DPF全等，根据全等三角形的对应边相等即可得证；

（2）可以用x表示PD进而表示AP，五边形面积y等于正方形面积减去两个全等三角形的面积，写得y的函数解析式．把函数解析式写出顶点式，结合x的取值范围求出y的取值范围．,

（1）∵四边形ABCD是正方形，

∴AB＝BC＝CD＝DA＝6，∠A＝∠D＝90°，

∴∠AEP＋∠APE＝90°，

∵PE⊥PF，

∴∠EPF＝90°，

∴∠APE＋∠DPF＝90°，

∴∠AEP＝∠DPF，

在△AEP与△DPF中，

，

∴△AEP≌△DPF（AAS），

∴AE=DP AP=DF，

∴DP+AP=AD=6；

（2）∵△AEP≌△DPF，

∴S△AEP＝S△DPF，DP＝AE＝x，

∴AP＝ADDP＝6x，

∴y＝S正方形ABCDS△AEP＝S△DPF＝S正方形ABCD2S△AEP＝AB22AEAP＝36x（6x）＝x26x＋36＝（x3）2＋27，

∵0＜x＜6，

∴x＝3时，y最小值为27；x＝0或6时，y＝（03）2＋27＝36，

∴27≤y＜36，

∴y＝x26x＋36，y的取值范围是27≤y＜36．