Question

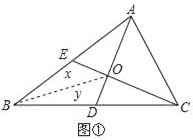
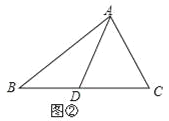
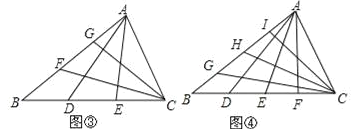
【题目】如图，分别以的斜边，直角边为边向外作等边和，为的中点，，相交于点.若∠BAC=30°，下列结论：①；②四边形为平行四边形；③；④.其中正确结论的序号是______.

Answer 1

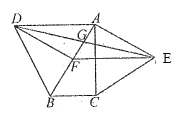
【答案】①②③④

【解析】

首先证明证明Rt△ADF≌Rt△BAC，结合已知得到AE=DF，然后根据内错角相等两直线平行得到DF∥AE，由一组对边平行且相等可得四边形ADFE是平行四边形，故②正确；由∠DAC=∠DAB+∠BAC=90°，可得∠AHE=90°，故①正确；由2AG=AF可知③正确；在Rt△DBF和Rt△EFA中，BD＝FE，DF＝EA，可证Rt△DBF≌Rt△EFA，故④正确.

∵△ABD和△ACE都是等边三角形，
∴AD=BD=AB，AE=CE=AC，∠ADB=∠BAD=∠DBA=∠CAE=∠AEC=∠ACE=60°．
∵F是AB的中点，

∴∠BDF=∠ADF=30°，∠DFA=∠DFB=90°，BF=AF=AB．
∵∠BAC=30°，∠ACB=90°，AD=2AF．
∴BC=AB，∠ADF=∠BAC，
∴AF=BF=BC．
在Rt△ADF和Rt△BAC中
AD＝BA ，AF＝BC，
∴Rt△ADF≌Rt△BAC（HL），
∴DF=AC，
∴AE=DF．
∵∠BAC=30°，
∴∠BAC+∠CAE=∠BAE=90°，
∴∠DFA=∠EAB，
∴DF∥AE，
∴四边形ADFE是平行四边形，故②正确；

∴AD=EF，AD∥EF，

设AC交EF于点H，
∴∠DAC=∠AHE．
∵∠DAC=∠DAB+∠BAC=90°，
∴∠AHE=90°，
∴EF⊥AC．①正确；
∵四边形ADFE是平行四边形，
∴2GF=2GA=AF．
∴AD=4AG．故③正确．
在Rt△DBF和Rt△EFA中
BD＝FE，DF＝EA，
∴Rt△DBF≌Rt△EFA（HL）．故④正确，
故答案为：①②③④．