Question

【题目】如图，在△ABC中，∠B＝90°，AB＝12米，BC＝24米，动点P从点A开始沿边AB向B以2米/秒的速度运动（不与点B重合），动点Q从点B开始沿BC向C以4米/秒的速度运动（不与点C重合）．如果P、Q分别从A、B同时出发，设运动时间为x秒，四边形APQC的面积为y平方米．

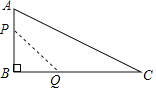
（1）求y与x之间的函数关系式，直接写出自变量x的取值范围；

（2）求当x为多少时，y有最小值，最小值是多少？

Answer 1

【答案】（1）0＜x＜6；（2）当x＝3时，y取得最小值，最小值为108

【解析】

（1）根据等量关系“四边形APQC的面积＝三角形ABC的面积﹣三角形PBQ的面积”列出函数关系；

（2）将函数解析式配方成顶点式，再根据二次函数的性质求最小值．

（1）根据题意知S＝S△ABC﹣S△PBQ

＝×12×24﹣×4x×（12﹣2x）

＝4x2﹣24x+144，

由12﹣2x＞0得x＜6，

∴0＜x＜6；

（2）y＝4x2﹣24x+144＝4（x﹣3）2+108．

∵4＞0

∴当x＝3时，y取得最小值，最小值为108．