题目内容
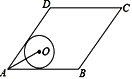
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,若AO=10,则⊙O的半径长为_______.
【答案】2![]()
【解析】分析:如图作DH⊥AB于H,连接BD,延长AO交BD于E.利用菱形的面积公式求出DH,再利用勾股定理求出AH,BD,由△AOF∽△DBH,可得![]() ,再将OA、BD、BH的长度代入即可求得OF的长度.
,再将OA、BD、BH的长度代入即可求得OF的长度.
详解:
如图所示:作DH⊥AB于H,连接BD,延长AO交BD于E.
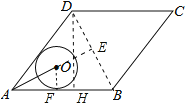
∵菱形ABCD的边AB=20,面积为320,
∴ABDH=320,
∴DH=16,
在Rt△ADH中,AH=![]()
∴HB=AB-AH=8,
在Rt△BDH中,BD=![]() ,
,
设⊙O与AB相切于F,连接OF.
∵AD=AB,OA平分∠DAB,
∴AE⊥BD,
∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,
∴△AOF∽△DBH,
∴![]() ,即
,即![]()
∴OF=2![]() .
.
故答案是:2![]() .
.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目