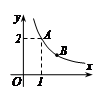题目内容
如图一次函数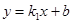 的图象与反比例函数
的图象与反比例函数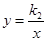 的图象交于点A
的图象交于点A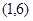 ,B(3,a).
,B(3,a).
(1)求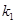 、
、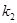 的值;
的值;
(2)直接写出一次函数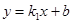 的值大于反比例函数
的值大于反比例函数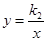 的值时x的取值范围:
的值时x的取值范围:
;
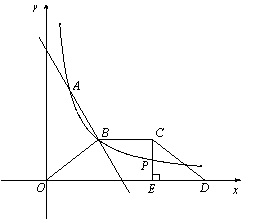
(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x 轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象 交于点P,当点P为CE的中点时,求梯形OBCD的面积.
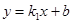 的图象与反比例函数
的图象与反比例函数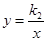 的图象交于点A
的图象交于点A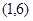 ,B(3,a).
,B(3,a).
(1)求
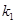 、
、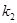 的值;
的值;(2)直接写出一次函数
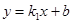 的值大于反比例函数
的值大于反比例函数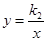 的值时x的取值范围:
的值时x的取值范围:;
(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x 轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象 交于点P,当点P为CE的中点时,求梯形OBCD的面积.
(1)k1=-2,k2=6(2)1<x<3 或 x<0(3)12
(1)把A 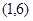 代入
代入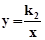 得:k2=6 ∴
得:k2=6 ∴ 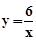 (1分)
(1分)
把B(3,a)代入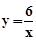 得:a=2 ∴B(3,
得:a=2 ∴B(3,
2) (1分)
把B(3,2)A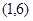 分别代入
分别代入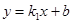 得:
得: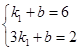
解得: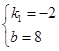
∴k1=-2 (2分)
(2)1<x<3 或 x<0 (2分)
(3) 等腰梯形OBCD中,BC//OD,OB=CD,OD边在x轴上且B(3,2)
设C(a,2) (1分)
∵CE⊥OD于点E,CE和反比例函数的图象交于点P, 点P为CE的中点,∴P(a,1) (1分)
把P(a,1)代入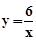 得:a=6 ∴C(6,2) ∴BC=3 (1分)
得:a=6 ∴C(6,2) ∴BC=3 (1分)
又∵OD=9 CE=2 (1分)
∴S梯形OBCD=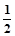 ×(9+3)×2=12 (2分)
×(9+3)×2=12 (2分)
(1)先把A(1,6)代入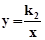 可求出k2=6,则反比例函数的解析式
可求出k2=6,则反比例函数的解析式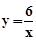 ,然后把B(3,a)代入
,然后把B(3,a)代入 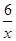 得a=2,确定B点坐标为(3,2),再利用待定系数法确定一次函数的解析式,从而得到k1的值;
得a=2,确定B点坐标为(3,2),再利用待定系数法确定一次函数的解析式,从而得到k1的值;
(2)观察图象得到当x<0或1<x<3时,一次函数的图象在反比例函数图象的上方;
(3)设C(t,2),过B作BF⊥x轴于F点,由点P为CE的中点得到P(t,1),又由点P在反比例函数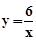 的图象上,易得C点坐标为(6,2),再利用OB=CD,OD边在x轴上且B(3,2),得到BC=3,ED=OF=3,则OD=OF+EF+ED=9,而CE=2,然后根据梯形的面积公式计算即可.
的图象上,易得C点坐标为(6,2),再利用OB=CD,OD边在x轴上且B(3,2),得到BC=3,ED=OF=3,则OD=OF+EF+ED=9,而CE=2,然后根据梯形的面积公式计算即可.
 代入
代入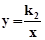 得:k2=6 ∴
得:k2=6 ∴ 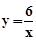 (1分)
(1分)把B(3,a)代入
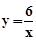 得:a=2 ∴B(3,
得:a=2 ∴B(3,2) (1分)
把B(3,2)A
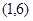 分别代入
分别代入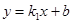 得:
得: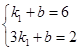
解得:
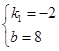
∴k1=-2 (2分)
(2)1<x<3 或 x<0 (2分)
(3) 等腰梯形OBCD中,BC//OD,OB=CD,OD边在x轴上且B(3,2)
设C(a,2) (1分)
∵CE⊥OD于点E,CE和反比例函数的图象交于点P, 点P为CE的中点,∴P(a,1) (1分)
把P(a,1)代入
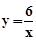 得:a=6 ∴C(6,2) ∴BC=3 (1分)
得:a=6 ∴C(6,2) ∴BC=3 (1分) 又∵OD=9 CE=2 (1分)
∴S梯形OBCD=
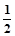 ×(9+3)×2=12 (2分)
×(9+3)×2=12 (2分)(1)先把A(1,6)代入
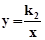 可求出k2=6,则反比例函数的解析式
可求出k2=6,则反比例函数的解析式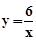 ,然后把B(3,a)代入
,然后把B(3,a)代入 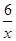 得a=2,确定B点坐标为(3,2),再利用待定系数法确定一次函数的解析式,从而得到k1的值;
得a=2,确定B点坐标为(3,2),再利用待定系数法确定一次函数的解析式,从而得到k1的值;(2)观察图象得到当x<0或1<x<3时,一次函数的图象在反比例函数图象的上方;
(3)设C(t,2),过B作BF⊥x轴于F点,由点P为CE的中点得到P(t,1),又由点P在反比例函数
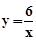 的图象上,易得C点坐标为(6,2),再利用OB=CD,OD边在x轴上且B(3,2),得到BC=3,ED=OF=3,则OD=OF+EF+ED=9,而CE=2,然后根据梯形的面积公式计算即可.
的图象上,易得C点坐标为(6,2),再利用OB=CD,OD边在x轴上且B(3,2),得到BC=3,ED=OF=3,则OD=OF+EF+ED=9,而CE=2,然后根据梯形的面积公式计算即可.
练习册系列答案
相关题目
 的—次函数
的—次函数 =
= 和反比例函数
和反比例函数 的图象都经过点(1,-2).求:
的图象都经过点(1,-2).求: 的图象经过点P,则k= .
的图象经过点P,则k= .
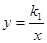 的图象与一次函数
的图象与一次函数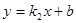 的图象交于
的图象交于 、
、 两点,
两点,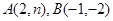 .
. 上是否存在一点
上是否存在一点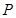 ,使
,使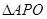 ∽
∽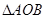 ,若存在,求
,若存在,求
 上的一点,PD⊥
上的一点,PD⊥ 轴于点D,则△POD的面积为 ;
轴于点D,则△POD的面积为 ;
 的图象上有两点A(
的图象上有两点A(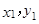 ),B(
),B( ),且
),且 ,那么下列结论正确的是
,那么下列结论正确的是 <
<
 (k≠0、x>0)相交,则该分支所在象限为 ( )
(k≠0、x>0)相交,则该分支所在象限为 ( )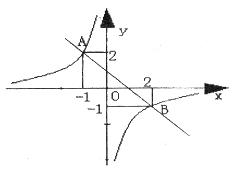
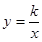 的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是_______________。
的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是_______________。