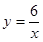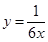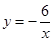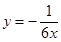题目内容
如图,已知反比例函数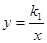 的图象与一次函数
的图象与一次函数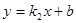 的图象交于
的图象交于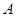 、
、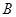 两点,
两点,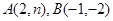 .
.
(1)求反比例函数和一次函数的关系式;
(2)在直线 上是否存在一点
上是否存在一点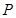 ,使
,使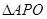 ∽
∽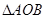 ,若存在,求
,若存在,求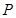 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.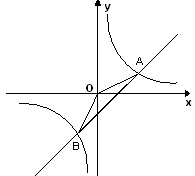
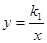 的图象与一次函数
的图象与一次函数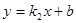 的图象交于
的图象交于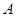 、
、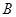 两点,
两点,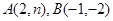 .
.(1)求反比例函数和一次函数的关系式;
(2)在直线
 上是否存在一点
上是否存在一点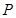 ,使
,使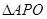 ∽
∽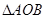 ,若存在,求
,若存在,求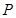 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
解:(1) ∵双曲线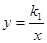 过点
过点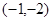
∴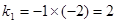
∵双曲线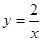 过点
过点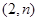
∴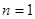
由直线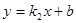 过点
过点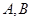 得
得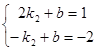 ,解得
,解得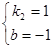
∴反比例函数关系式为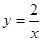 ,一次函数关系式为
,一次函数关系式为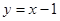 .
.
(2)存在符合条件的点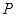 ,
,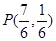 .理由如下:
.理由如下:
∵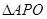 ∽
∽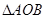
∴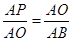 ∴
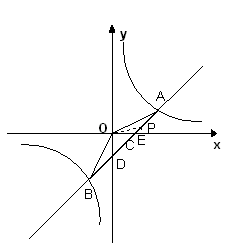
∴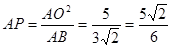 ,如右图,设直线
,如右图,设直线 与
与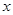 轴、
轴、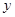 轴分别相交于点
轴分别相交于点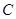 、
、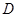 ,过
,过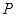 点作
点作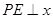 轴于点
轴于点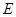 ,连接
,连接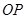 ,则
,则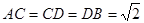 ,
,
故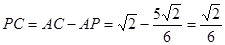 ,再由
,再由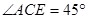 得
得 ,
,
从而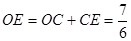 ,因此,点
,因此,点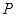 的坐标为
的坐标为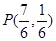 .
.
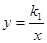 过点
过点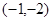
∴
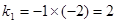
∵双曲线
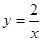 过点
过点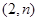
∴
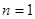
由直线
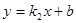 过点
过点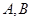 得
得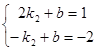 ,解得
,解得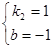
∴反比例函数关系式为
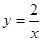 ,一次函数关系式为
,一次函数关系式为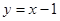 .
.(2)存在符合条件的点
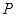 ,
,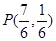 .理由如下:
.理由如下:∵
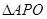 ∽
∽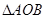
∴
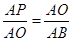 ∴
∴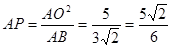 ,如右图,设直线
,如右图,设直线 与
与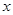 轴、
轴、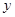 轴分别相交于点
轴分别相交于点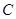 、
、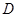 ,过
,过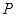 点作
点作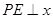 轴于点
轴于点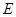 ,连接
,连接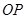 ,则
,则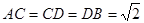 ,
,
故
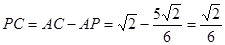 ,再由
,再由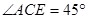 得
得 ,
,从而
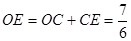 ,因此,点
,因此,点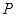 的坐标为
的坐标为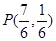 .
.(1)先根据反比例函数求出点A的坐标,再由A、B的坐标根据待定系数法即可求得一次函数解析式;
(2)由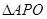 ∽
∽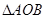 ,根据对应边成比例即可求出AP的长,再根据一次函数求出与坐标轴的交点坐标,即得AC、CD、DB、PC的长,再由
,根据对应边成比例即可求出AP的长,再根据一次函数求出与坐标轴的交点坐标,即得AC、CD、DB、PC的长,再由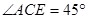 求得CE、PE的长即可求得点P的坐标。
求得CE、PE的长即可求得点P的坐标。
(2)由
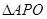 ∽
∽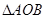 ,根据对应边成比例即可求出AP的长,再根据一次函数求出与坐标轴的交点坐标,即得AC、CD、DB、PC的长,再由
,根据对应边成比例即可求出AP的长,再根据一次函数求出与坐标轴的交点坐标,即得AC、CD、DB、PC的长,再由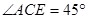 求得CE、PE的长即可求得点P的坐标。
求得CE、PE的长即可求得点P的坐标。
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
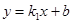 的图象与反比例函数
的图象与反比例函数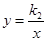 的图象交于点A
的图象交于点A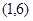 ,B(3,a).
,B(3,a).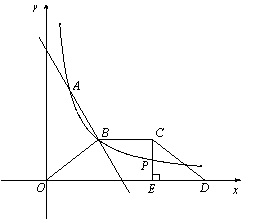
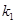 、
、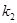 的值;
的值; 轴、
轴、 轴上的动点,点C、D是某函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。如图,正方形ABCD是反比例函数
轴上的动点,点C、D是某函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。如图,正方形ABCD是反比例函数 图像上的其中一个伴侣正方形。则这个伴侣正方形的边长是____________;
图像上的其中一个伴侣正方形。则这个伴侣正方形的边长是____________;
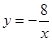 与一次函数
与一次函数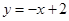 交于
交于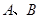 两点,O为坐标原点,则
两点,O为坐标原点,则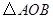 的面积为( )
的面积为( )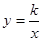 (k>0)的图象与AC边交于点E.
(k>0)的图象与AC边交于点E.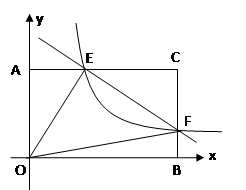
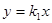 与双曲线y=
与双曲线y=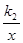 有一交点为(
有一交点为(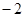 ,4),则另一交点坐标是______。
,4),则另一交点坐标是______。 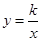 的图象经过点(
的图象经过点(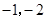 ),则
),则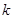 的值为 .
的值为 . 的自变量
的自变量 的取值范围是 ▲ .
的取值范围是 ▲ .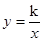 ,若
,若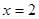 时,
时,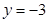 ,则这个函数的解析式是 ( )
,则这个函数的解析式是 ( )