题目内容
49、如图，已知平行四边形ABCD，AE平分∠DAB交DC于E，BF平分∠ABC交DC于F，DC=6cm，AD=2cm，求DE、EF、FC的长．分析：因为平行四边形对边平行，所以∠1=∠2，又因为∠1=∠3，所以DE=AD=2，同理FC=BC=2，又DC=6，所以EF=2．
解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD=BC，
∴∠1=∠2，
又∵AE平分∠DAB，
∴∠1=∠3，
∴∠2=∠3，
∴DA=DE=2cm
同理BC=CF=2cm．
∴EF=DC-DE-CF=6cm-2cm-2cm=2cm．
∴AB∥CD，AD=BC，
∴∠1=∠2，
又∵AE平分∠DAB，
∴∠1=∠3，
∴∠2=∠3，
∴DA=DE=2cm
同理BC=CF=2cm．
∴EF=DC-DE-CF=6cm-2cm-2cm=2cm．
点评：本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．
练习册系列答案
计算高手系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．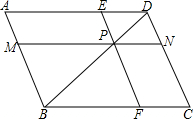
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．