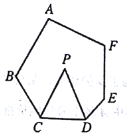
题目内容
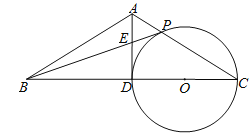
【题目】已知:如图,在△ABC中,AB=AC,点D是边BC的中点,以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
【答案】(1) 证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由AB=AC,点D是BC的中点可得AD⊥BC,结合CD是⊙O的直径,即可得AD是⊙O的切线;
(2)连接OP,由已知易求得BD、OB、OP和BP的长,再证PE=DE,△BDE∽△BPO即可列出比例式求得DE的长,从而可得PE的长.
试题解析:
(1)∵AB=AC,点D是边BC的中点,
∴AD⊥CD,
∵CD为⊙O的直径,
∴AD是⊙O的切线;
(2)连接OP,
∵点D是边BC的中点,BC=4,CD是⊙O的直径,
∴CD=BD=2,OP=1,OB=3,
∴在Rt△BOP中,BP=![]() ,
,
∵AD是⊙O的切线,PB是⊙O的切线,
∴PE=DE,∠BPO=90°,
∵AD⊥CD,
∴∠ADB=∠BPO=90°,
又∵∠DBE=∠PBO,
∴△BDE∽△BPO,
∴![]() ,即
,即![]() ,解得:DE=
,解得:DE=![]() ,
,
∴PE=DE=![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目