题目内容
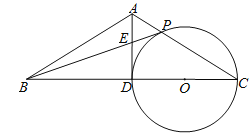
【题目】如图,二次函数![]() 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式及顶点坐标;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在抛物线的对称轴上是否存在一点P.使得以O、B、C、P四点为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.

【答案】(1)(4,2);(2)6;(3)存在, P1(2,6),P2(2,-6)
【解析】试题分析:(1)题利用待定系数法求出解析式;
(2)以AC为三角形的底,OB为三角形的高,求出三角形的底与高就可以求出,三角形面积;
(3)分两种情况讨论即可.
试题解析:解:(1)将A(2,0)、B(0,﹣6)两点代入则:
![]() ,解得:
,解得: ![]() ,∴解析式为y=
,∴解析式为y=![]() x2+4x﹣6,∵y=
x2+4x﹣6,∵y=![]() x2+4x﹣6=
x2+4x﹣6=![]() ,∴顶点坐标为:(4,2);
,∴顶点坐标为:(4,2);
(2)令![]() x2+4x﹣6=0,∴x2﹣8x+12=0,∴解得:x1=2,x2=6,∴另一个交点C(6,0),
x2+4x﹣6=0,∴x2﹣8x+12=0,∴解得:x1=2,x2=6,∴另一个交点C(6,0),
∴AC=2,∴S△ABC=![]() ×2×6=6;
×2×6=6;
(3)存在.分两种情况讨论:
①显然过B作BP∥OC交对称轴于点P,则四边形OBPC是矩形,此时P(2,-6);
②过O作OP∥BC交对称轴于点P,∵OB∥PC,∴四边形OBCP是平行四边形,∴CP=OB=6,∴P(2,6).
综上所述:P(2,6)或P(2,-6).


练习册系列答案
相关题目