��Ŀ����
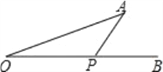
����Ŀ������������8�֣���֪����ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ����Խ���������⣺

��1����ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ���� ����
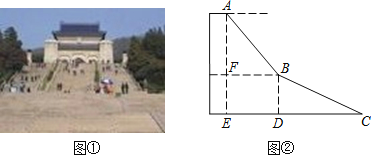
��2����ϸ�۲죬��ͼ2�С�8���Ρ��ĸ������� ������
��3����ͼ2�У�����D=40������B=36������DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N�����ã�1���Ľ��ۣ�����á�P�Ķ������� ����
��4�����ͼ2�С�D�͡�BΪ�����ʱ�������������䣬��ֱ��д����P���D����B֮����ڵ�������ϵ���� ����
���𰸡���1����A+��D=��C+��B��2��6����3��45����4��2��P=��D+��B
���������������:��1�����������ε��ڽǺͶ�����ʾ����AOD����BOC���ٸ��ݶԶ�����ȿɵ���AOD=��BOC��Ȼ���������ɵý⣻
��2��������8�������Ľṹ�ص㣬���ݽ���д����8�������������Σ�Ȼ��ȷ�����ɣ�
��3�����ݣ�1���Ĺ�ϵʽ�����OCB����OAD���ٸ��ݽ�ƽ���ߵĶ��������DAM����PCM��Ȼ��������8�������Ĺ�ϵʽ��ʽ�������ɵý⣻
��4��������8����������B����D��ʾ����OCB����OAD��������D����P��ʾ����DAM����PCM��Ȼ����ݽ�ƽ���ߵĶ���ɵ���DAM����PCM=![]() ����OCB����OAD����Ȼ���������ɵ�֤��
����OCB����OAD����Ȼ���������ɵ�֤��
�⣺��1������AOD�У���AOD=180�㩁��A����D��
����BOC�У���BOC=180�㩁��B����C��
�ߡ�AOD=��BOC���Զ�����ȣ���
��180�㩁��A����D=180�㩁��B����C��
���A+��D=��B+��C��
��2�������е�M��O��N��
��M������1������AMD����CMP��
��O������4������AOD����COB����AOM����CON����AOM����COB����CON����AOD��
��N������1������ANP����CNB��
���ԣ���8������ͼ�ι���6����
��3���ߡ�D=40������B=36����
���OAD+40��=��OCB+36����
���OCB����OAD=4����
��AP��CP�ֱ�����DAB����BCD�Ľ�ƽ���ߣ�
���DAM=![]() ��OAD����PCM=
��OAD����PCM=![]() ��OCB��
��OCB��
���ߡ�DAM+��D=��PCM+��P��
���P=��DAM+��D����PCM=![]() ����OAD����OCB��+��D=
����OAD����OCB��+��D=![]() ������4����+40��=38����
������4����+40��=38����
��4��������8������������ϵ����OAD+��D=��OCB+��B����DAM+��D=��PCM+��P��
���ԣ���OCB����OAD=��D����B����PCM����DAM=��D����P��
��AP��CP�ֱ�����DAB����BCD�Ľ�ƽ���ߣ�
���DAM=![]() ��OAD����PCM=
��OAD����PCM=![]() ��OCB��
��OCB��
��![]() ����D����B��=��D����P��
����D����B��=��D����P��
�����ã�2��P=��B+��D��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�