题目内容
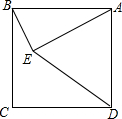
如图,已知正方形ABCD和正方形CGEF(CG>BC),B、C、G在同一直线上,M为线段AE的中点,试问:线段MD与线段MF的大小关系,并证明你的结论.


答:MF=MD.
证明:延长DM交EF于点P,
∵四边形ABCD和四边形FCGE是正方形,
∴AD∥EF,∠MAD=∠MEP.∠CFE=90°.
∴△DFP是直角三角形.
∵M为AE的中点,
∴AM=EM.
∵在△ADM和△EPM中,
,
∴△ADM≌△EPM(ASA),
∴DM=PM.
∴M是DP的中点.
∴MF=
DP=MD.

证明:延长DM交EF于点P,
∵四边形ABCD和四边形FCGE是正方形,
∴AD∥EF,∠MAD=∠MEP.∠CFE=90°.
∴△DFP是直角三角形.
∵M为AE的中点,
∴AM=EM.
∵在△ADM和△EPM中,
|
∴△ADM≌△EPM(ASA),
∴DM=PM.
∴M是DP的中点.
∴MF=
| 1 |
| 2 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目