Question

已知，如图1，正方形ABCD和正方形BEFG，三点A、B、E在同一直线上，连接AG和CE，
（1）判定线段AG和线段CE的数量有什么关系？请说明理由．
（2）将正方形BEFG，绕点顺时针旋转到图2的位置时，（1）中的结论是否成立？请说明理由．
（3）若在图2中连接AE和CG，且AE=2CG=4，求正方形ABCD和正方形BEFG的面积之和为______．（直接写出结果）．

Answer 1

（1）AG=CE．
理由如下：在正方形ABCD和正方形BEFG中，AB=CB，BG=BE，∠ABG=∠CBE=90°，
在△ABG和△CBE中，
∵

AB=CB ∠ABG=∠CBE=90° BG=BE

，
∴△ABG≌△CBE（SAS），
∴AG=CE；

（2）AG=CE仍然成立．
理由如下：在正方形ABCD和正方形BEFG中，AB=CB，BG=BE，∠ABC=∠EBG=90°，
∵∠ABG=∠ABC+∠CBG，
∠CBE=∠EBG+∠CBG，
∴∠ABG=∠CBE，
在△ABG和△CBE中，
∵

AB=CB ∠ABG=∠CBE BG=BE

，
∴△ABG≌△CBE（SAS），
∴AG=CE；

（3）如图2，连接AC、EG，设AG、CE交点为H，
∵△ABG≌△CBE，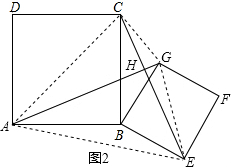
∴∠BAG=∠BCE，
∴∠CAH+∠ACH=∠CAH+∠ACB+∠BCE
=∠CAH+∠ACB+∠BAG=90°，
∴AG⊥CE，
在Rt△CGH中，CG²=CH²+GH²，
在Rt△AEH中，AE²=AH²+EH²，
∴CG²+AE²=CH²+GH²+AH²+EH²=（CH²+AH²）+（GH²+EH²）=AC²+EG²，
∵AE=2CG=4，
∴CG=2，
∴AC²+EG²=2²+4²=20，
∴正方形ABCD和正方形BEFG的面积之和为

1

2

×20=10．
故答案为：10．