题目内容
【题目】综合与探究
已知:![]() 、
、![]() 是方程
是方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图像经过点
的图像经过点![]() 、
、![]() .
.
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与![]() 轴的另一交点为
轴的另一交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,试求出点
,试求出点![]() 、
、![]() 的坐标和
的坐标和![]() 的面积;
的面积;
(3)![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作
作![]() 轴,与抛物线交于
轴,与抛物线交于![]() 点,若直线
点,若直线![]() 把
把![]() 分成面积之比为
分成面积之比为![]() 的两部分,请直接写出
的两部分,请直接写出![]() 点的坐标 ;
点的坐标 ;
(4)若点![]() 在直线
在直线![]() 上,点
上,点![]() 在平面上,直线
在平面上,直线![]() 上是否存在点
上是否存在点![]() ,使以点
,使以点![]() 、点
、点![]() 、点
、点![]() 、点
、点![]() 为顶点的四边形为菱形?若存在,请直接写出点
为顶点的四边形为菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
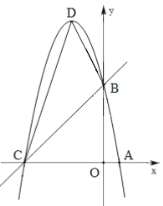
【答案】(1)y=x24x+5;(2)15;(3)(![]() ,0)或(
,0)或(![]() ,0);(4)存在M点,M点坐标为(7,12)或
,0);(4)存在M点,M点坐标为(7,12)或![]()
【解析】
(1)通过解方程即可求出p、q的值,那么A、B两点的坐标就可求出.然后根据A、B两点的坐标即可求出抛物线的解析式.
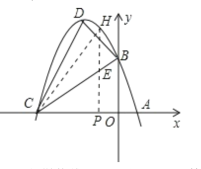
(2)根据(1)得出的抛物线的解析式即可求出C、D两点的坐标.由于△BCD的面积无法直接求出,可用其他图形的面积的“和,差关系”来求出.过D作DM⊥x轴于M,那么△BCD的面积=梯形DMOB的面积+△DCM的面积-△BOC的面积.由此可求出△BCD的面积.
(3)由于△PCH被直线BC分成的两个小三角形等高,因此面积比就等于底边的比.如果设PH与BC的交点为E,那么EH就是抛物线与直线BC的函数值的差,而EP就是E点的纵坐标.然后可根据直线BC的解析式设出E点的坐标,然后表示出EH,EP的长.进而可分两种情况进行讨论:①当EH=![]() EP时;②当EH=
EP时;②当EH=![]() EP时.由此可得出两个不同的关于E点横坐标的方程即可求出E点的坐标.也就求出了P点的坐标.
EP时.由此可得出两个不同的关于E点横坐标的方程即可求出E点的坐标.也就求出了P点的坐标.
(4)分两种情况讨论,当CD=DM和当![]() 时,根据M点在直线BC上设出M点坐标,根据两点间距离公式列出方程即可求解出M点坐标.
时,根据M点在直线BC上设出M点坐标,根据两点间距离公式列出方程即可求解出M点坐标.
解方程x26x+5=0,
(x1)(x5)=0,
得x1=5,x2=1
∵![]() ,
,
∴p=1,q=5
∴点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入y=x2+bx+c.
得![]()
得:![]()
∴抛物线的解析式为y=x24x+5
故答案为:y=x24x+5
(2)∵y=x24x+5,
令y=0,得x24x+5=0,
得x1=5,x2=1,
∴C点的坐标为(5,0)
∵![]() ,
,![]()
∴点D(2,9)
过D作x轴的垂线交x轴于M
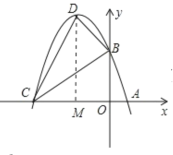
∴S△DMC=![]() ×9×(52)=
×9×(52)=![]()
S梯形MDBO=![]() ×2×(9+5)=14,
×2×(9+5)=14,
S△BOC=![]() ×5×5=
×5×5=![]()
∴S△BCD=S梯形MDBO+S△DMCS△BOC=14+![]()
![]() =15
=15
故答案为:15
(3)设P点的坐标为(a,0)
∵B(0,5),C (5,0)
设BC直线的解析式为y=kx+b
∴![]()
∴![]()
∴BC所在的直线解析式为y=x+5
设PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线y=x24x+5的交点坐标为H(a,a24a+5)
∵①EH=![]() EP,
EP,
即(a24a+5)(a+5)=![]() (a+5)
(a+5)
∴a=![]() 或a=5(舍去)
或a=5(舍去)
②EH=![]() EP,
EP,
即(a24a+5)(a+5)=![]() (a+5)
(a+5)
∴a=![]() 或a=5(舍去),
或a=5(舍去),
P点的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
故答案为:(![]() ,0)或(
,0)或(![]() ,0)
,0)
(4)①∵M在直线BC上,设M(m,m+5)
若使四边形CDMN为菱形,则CD=DM
∵C(-5,0),D(-2,9)
∴![]()
解得m=-5或m=7
m=-5时,恰好为C点,不符合题意舍去
∴m=7
∴M(7,12)
②∵直线BC上存在一点![]() ,设
,设![]()
若使四边形![]() 是菱形,则
是菱形,则![]()
∵C(-5,0),D(-2,9)
∴![]()
解得![]()
∴![]()
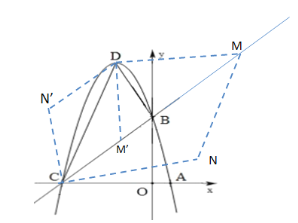
综上所述在直线BC上存在一点M,且以点![]() 、点
、点![]() 、点
、点![]() 、点
、点![]() 为顶点的四边形为菱形,此时M点坐标为(7,12)或
为顶点的四边形为菱形,此时M点坐标为(7,12)或![]()
故答案为:存在M点,M点坐标为(7,12)或![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案