��Ŀ����
����Ŀ����ͼ�٣��ھ���![]() �У���
����![]() ��
��![]() �ߵ��е�
�ߵ��е�![]() ����������
����������![]() ���˶����ٶ�Ϊÿ��2����λ���ȣ������
���˶����ٶ�Ϊÿ��2����λ���ȣ������![]() ��ֹͣ�˶�����
��ֹͣ�˶�����![]() ��
��![]() �ϵĵ㣬
�ϵĵ㣬![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() �룬
�룬![]() ��
��![]() �ĺ�����ϵ��ͼ����ʾ.
�ĺ�����ϵ��ͼ����ʾ.
(1)ͼ����![]() = ��
= ��![]() = ��ͼ����
= ��ͼ����![]() = .
= .
(2)��![]() =1��ʱ�����ж���
=1��ʱ�����ж���![]() Ϊֱ����Բ�Ƿ���
Ϊֱ����Բ�Ƿ���![]() ������?��˵������:
������?��˵������:
(3)��![]() ���˶������У���������
���˶������У���������![]() ����ֱ���۵�����
����ֱ���۵�����![]() Ϊ��ֵʱ���۵���
Ϊ��ֵʱ���۵���![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ���ھ��ε�һ����.
���ھ��ε�һ����.
���𰸡�(1)8,18,20;(2)�����У�֤������������3��t=![]() ��5��
��5��![]() .
.
��������
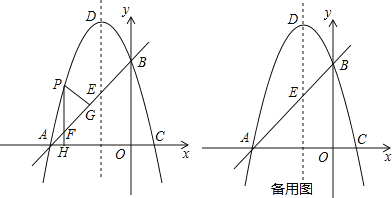
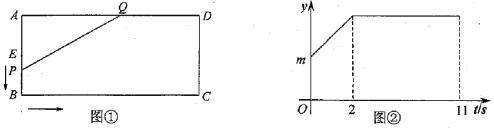
��1��������ó�AB=2BE��t=2ʱ��BE=2��2=4�����AB=2BE=8��AE=BE=4��t=11ʱ��2t=22���ó�BC=18����t=0ʱ����P��E����m=��AEQ�����=![]() AQ��AE=20���ɣ�
AQ��AE=20���ɣ�
��2����t=1ʱ��PE=2���ó�AP=AE+PE=6���ɹ��ɶ������PQ=2![]() ������PQΪֱ����Բ��Բ��ΪO'����O'N��BC��N���ӳ�NO'��AD��M����MN=AB=8��O'M��AB��MN=AB=8������������λ�߶����ó�O'M=
������PQΪֱ����Բ��Բ��ΪO'����O'N��BC��N���ӳ�NO'��AD��M����MN=AB=8��O'M��AB��MN=AB=8������������λ�߶����ó�O'M=![]() AP=3�����O'N=MN-O'M=5��ԲO'�İ뾶�����ɵó����ۣ�
AP=3�����O'N=MN-O'M=5��ԲO'�İ뾶�����ɵó����ۣ�
��3��������������ٵ���P��AB���ϣ�A'����BC����ʱ����QF��BC��F����QF=AB=8��BF=AQ=10�����۵������ʵã�PA'=PA��A'Q=AQ=10����PA'Q=��A=90�����ɹ��ɶ������A'F=![]() =6���ó�A'B=BF-A'F=4����Rt��A'BP�У�BP=4-2t��PA'=AP=8-��4-2t��=4+2t���ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
=6���ó�A'B=BF-A'F=4����Rt��A'BP�У�BP=4-2t��PA'=AP=8-��4-2t��=4+2t���ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
�ڵ���P��BC���ϣ�A'����BC����ʱ�����۵������ʵã�A'P=AP��֤����APQ=��AQP���ó�AP=AQ=A'P=10����Rt��ABP�У��ɹ��ɶ������BP=6����BP=2t-4���ó�2t-4=6���ⷽ�̼��ɣ�
�۵���P��BC���ϣ�A'����CD����ʱ�����۵������ʵã�A'P=AP��A'Q=AQ=10����Rt��DQA'�У�DQ=AD-AQ=8���ɹ��ɶ������DA'=6���ó�A'C=CD-DA'=2����Rt��ABP��Rt��A'PC�У�BP=2t-4��CP=BC-BP=22-2t���ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
��1���ߵ�P��AB�ߵ��е�E�������ٶ�Ϊÿ��2����λ���ȣ�
��AB=2BE��
��ͼ��ã�t=2ʱ��BE=2��2=4��
��AB=2BE=8��AE=BE=4��
t=11ʱ��2t=22��
��BC=22-4=18��
��t=0ʱ����P��E����m=��AEQ�����=![]() AQ��AE=
AQ��AE=![]() ��10��4=20��
��10��4=20��
�ʴ�Ϊ��8��18��20��
��2����t=1��ʱ����PQΪֱ����Բ����BC�����У��������£�
��t=1ʱ��PE=2��
��AP=AE+PE=4+2=6��
���ı���ABCD�Ǿ��Σ�
���A=90����
��PQ=![]() ��
��
����PQΪֱ����Բ��Բ��ΪO'����O'N��BC��N���ӳ�NO'��AD��M����ͼ1��ʾ��
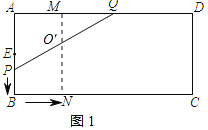
��MN=AB=8��O'M��AB��MN=AB=8��
��O'ΪPQ���е㣬
��O'M����APQ����λ�ߣ�
��O'M=![]() AP=3��
AP=3��
��O'N=MN-O'M=5��![]() ��
��
����PQΪֱ����Բ����BC�����У�
��3��������������ٵ���P��AB���ϣ�A'����BC����ʱ����QF��BC��F����ͼ2��ʾ��
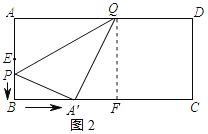
��QF=AB=8��BF=AQ=10��
���ı���ABCD�Ǿ��Σ�
���A=��B=��BCD=��D=90����CD=AB=8��AD=BC=18��
���۵������ʵã�PA'=PA��A'Q=AQ=10����PA'Q=��A=90����
��A'F=![]() =6��
=6��
��A'B=BF-A'F=4��
��Rt��A'BP��BP=4-2t��PA'=AP=8-��4-2t��=4+2t��
�ɹ��ɶ����ã�42+��4-2t��2=��4+2t��2��
��ã�t=![]() ��
��
�ڵ���P��BC���ϣ�A'����BC����ʱ������AA'����ͼ3��ʾ��
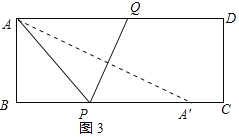
���۵������ʵã�A'P=AP��
���APQ'=��A'PQ��
��AD��BC��
���AQP=��A'PQ��
���APQ=��AQP��
��AP=AQ=A'P=10��
��Rt��ABP�У��ɹ��ɶ����ã�BP=![]() =6��
=6��
�֡�BP=2t-4��
��2t-4=6����ã�t=5��
�۵���P��BC���ϣ�A'����CD����ʱ������AP��A'P����ͼ4��ʾ��

���۵������ʵã�A'P=AP��A'Q=AQ=10��
��Rt��DQA'��DQ=AD-AQ=8��
�ɹ��ɶ����ã�DA'=![]() =6��
=6��
��A'C=CD-DA'=2��
��Rt��ABP��Rt��A'PC��BP=2t-4��CP=BC-BP=18-��2t-4��=22-2t��
�ɹ��ɶ����ã�AP2=82+��2t-4��2��A'P2=22+��22-2t��2��
��82+��2t-4��2=22+��22-2t��2��
��ã�t=![]() ��
��
����������tΪ![]() ��5��
��5��![]() ʱ���۵���A�Ķ�Ӧ��A�����ھ��ε�һ���ϣ�
ʱ���۵���A�Ķ�Ӧ��A�����ھ��ε�һ���ϣ�

����Ŀ���ס��ҡ�����λ�˶�Ա����ͬ�����¸����![]() �Σ�ÿ����еijɼ����£�
�Σ�ÿ����еijɼ����£�
�ף�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�ң�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��1������������������±���
ƽ���� | ��λ�� | ���� | |
�� |
|
| |
�� |
|
| |
�� |
|
|
��2������ʱ�������γ�����˳���ɳ�ǩ��ʽ��������ס������ڳ����ĸ��ʣ�