题目内容
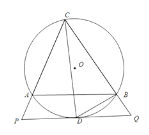
【题目】如图，△ABC内接于圆O，CD平分∠ACB交于圆O，过点D作PQ∥AB分别交CA、CB延长线于P、Q，连接BD．
(1)求证：PQ是圆O的切线；
(2)连接AD，求证：
【答案】（1）详见解析；（2）详见解析
【解析】
（1）连接OD，根据角平分线的性质和圆的基本性质可得
，然后根据垂径定理的推论可得OD垂直平分AB，从而证出OD⊥PQ，然后根据切线的判定定理即可证出结论；
（2）连接AD、BD，由（1）的结论可得AD=BD，∠BDQ=∠ACD，然后根据圆的内接四边形的性质可得∠DBQ=∠CAD，从而证出△DBQ∽△CAD，列出比例式即可证出结论．
证明：（1）连接OD
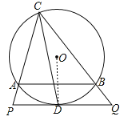
∵CD平分∠ACB交于圆O，
∴∠ACD=∠BCD
∴
∴OD垂直平分AB
∵PQ∥AB
∴OD⊥PQ
∴PQ是圆O的切线；
（2）连接AD、BD
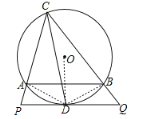
由（1）知，PQ是圆O的切线
∴AD=BD，∠BDQ=∠ACD
∵四边形ADBC为圆的内接四边形
∴∠DBQ=∠CAD
∴△DBQ∽△CAD
∴
∴
练习册系列答案
科学实验活动册系列答案
相关题目
