题目内容
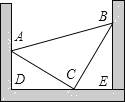
【题目】如图,一个等腰直角三角形零件放置在一凹槽内,顶点A.B.C分别落在凹槽内壁上,测得AD=5cm,BE=9cm,则该零件的面积为 _______
【答案】53cm2
【解析】
首先证明△ADC≌△CEB,根据全等三角形的性质可得DC=BE=9cm,再利用勾股定理计算出AC长,然后利用三角形的面积公式计算出该零件的面积即可.
解:∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵∠ADC=90°,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,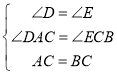 ,
,
∴△ADC≌△CEB(AAS),
∴DC=BE=9cm,
∴AC=![]() =
=![]() =
=![]() (cm),
(cm),
∴BC=![]() cm,
cm,
∴该零件的面积为:![]() ×
×![]() ×
×![]() =53(cm2).
=53(cm2).
故答案为:53cm2.

练习册系列答案
相关题目
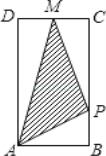
【题目】如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A B C M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
A.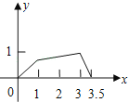 B.
B.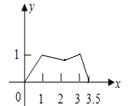 C.
C.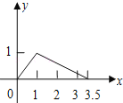 D.
D.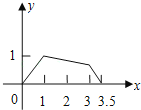
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.