题目内容
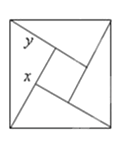
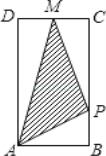
【题目】如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A B C M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
A.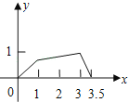 B.
B.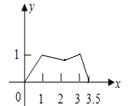 C.
C.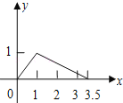 D.
D.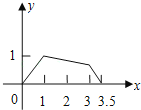
【答案】B
【解析】
根据每一段函数的性质,确定其解析式,特别注意根据函数的增减性,以及几个最值点,确定选项比较简单.
①当P在AB上运动时,
所求三角形底为AP,高为M到AB的距离也就是AD长度
因此S![]() =
=![]() ADAP=x,
ADAP=x,
函数关系为:y=x(0<x1);
②当P在BC上运动时,
S![]() =S梯形ABCMS
=S梯形ABCMS![]() S
S![]()
S![]() =
=![]() ABBP,
ABBP,
BP=x1,
则S![]() =
=![]() x
x![]() ,
,
S![]() =12PCCM,
=12PCCM,
CM=DM=![]() ,PC=3x,
,PC=3x,
S![]() =
=![]() ,
,
S梯形ABCM=![]() (AB+CM)BC=
(AB+CM)BC=![]() ,
,
因此S![]() =
=![]() (1<x3);
(1<x3);
③当P在CM上运动时,
S![]() =
=![]() CMAD,
CMAD,
CM=![]() x,
x,
S![]() =
=![]() (3<x<
(3<x<![]() ).
).
故该图象分三段.
故选B.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
【题目】在一次为地震灾区的捐款活动中,某校随机调查了50名学生的捐款情况,统计如表:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 10 | 12 | 3 |
(1)这50名学生捐款金额的众数和中位数分别为多少元?
(2)如果把这50名学生的捐款情况绘制成扇形统计图,则捐款金额为15元的人数所对应的扇形圆心角为多少度?
(3)若该校共有1200名学生,估计该校的捐款总数大约是多少元?