题目内容
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上(点
上(点![]() 不与
不与![]() ,
,![]() 重合),直线
重合),直线![]() 交过点
交过点![]() 的切线于点
的切线于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() .
.
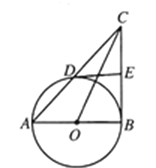
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析; (2) ![]() 的值为
的值为![]() .
.
【解析】
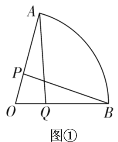
(1)证明:连接OD,如图,利用切线长定理得到EB=ED,利用切线的性质得OD⊥DE,AB⊥CB,再根据等角的余角相等得到∠CDE=∠ACB,则EC=ED,从而得到BE=CE;
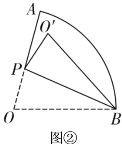
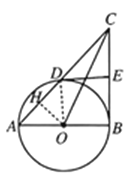
(2)作OH⊥AD于H,如图,设⊙O的半径为r,先证明四边形OBED为正方形得DE=CE=r,再利用△AOD和△CDE都为等腰直角三角形得到OH=DH= ![]() r,CD=
r,CD= ![]() r,接着根据勾股定理计算出OC=
r,接着根据勾股定理计算出OC=![]() r,然后根据正弦的定义求解.
r,然后根据正弦的定义求解.
解:(1)连接![]() ,如图.
,如图.
![]() 为
为![]() 的切线,.
的切线,.
∴![]() ,
,![]() ,.
,.
![]() ,
,![]()
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]()
(2)如图,作![]() 于点
于点![]() .
.
设![]() 的半径为
的半径为![]() ,
,
![]() ,
,
![]()
∴四边形![]() 为矩形,
为矩形,
又![]() ,
,
∴四边形![]() 为正方形
为正方形
![]() .
.
易得![]() 和
和![]() 都为等腰直角三角形.
都为等腰直角三角形.
![]()
在![]() 中,
中,![]()
在![]() 中,
中,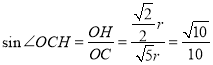
即![]() 的值为
的值为![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目