Question

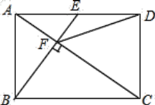
【题目】如图，在矩形中，是边的中点，，垂足为点，连接，有下列五个结论：①；②；③；④；⑤．其中正确结论的个数是( )

A.1B.C.D.

Answer 1

【答案】D

【解析】

①四边形ABCD是矩形，BE⊥AC，则∠ABC=∠AFB=90°，又∠BAF=∠CAB，于是△AEF∽△CAB；

②由，又AD∥BC，所以，故可得CF=2AE；

③过D作DM∥BE交AC于N，得到四边形BMDE是平行四边形，求出，得到CN=NF，根据线段的垂直平分线的性质可得结论；

④设AE=a，AB=b，则AD=2a，由△BAE∽△ADC，得出，进而得出；

⑤由AE∥BC，推出，设S△AEF=S△DEF=m，推出S△ABF=2m，S△BFC=4m，S矩形ABCD=12m，S矩形BCDF=8m，推出S△ABF：S四边形BCDF=1：4，故⑤正确

∵四边形ABCD是矩形，

∴AD∥BC，∠ABC=90°，AD=BC，

∵BE⊥AC于点F，

∴∠EAC=∠ACB，∠ABC=∠AFE=90°，

∴△AEF∽△CAB，故①正确；

∵AD∥BC，

∴△AEF∽△CBF，

∴，

∵AE=AD=BC，

∴，

∴CF=2AF，故②正确；

如图，过D作DM∥BE交AC于N，

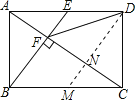
∵DE∥BM，BE∥DM，

∴四边形BMDE是平行四边形，

∴BM=DE=BC，

∴BM=CM，

∴CN=NF，

∵BE⊥AC于点F，DM∥BE，

∴DN⊥CF，

∴DM垂直平分CF，

∴DF=DC，故③正确；

设AE=a，AB=b，则AD=2a，

由△BAE∽△ADC，有，即，

所以，b=，

∴，故④错误；

，

，

设，

，，，，

故⑤正确；

故选：D．