题目内容
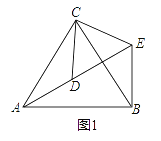
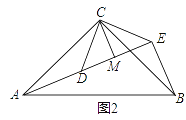
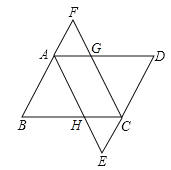
【题目】如图,四边形ABCD为平行四边形,∠BAD和∠BCD的平分线AE,CF分别交DC,BA的延长线于点E,F,交边BC,AD于点H,G.
(1)求证:四边形AECF是平行四边形.
(2)若AB=5,BC=8,求AF+AG的值.
【答案】(1)证明见解析;(2)6.
【解析】
(1)由平行四边形的性质,结合角平分线的定义可证得AE∥CF,结合AF∥CE,可证得结论;
(2)由条件可证得△DCG∽△AFG,利用相似三角形的性质可求得DG与AG的关系,结合条件可求得AG的长,从而可求得答案.
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∵AE、CF分别平分∠BAD∠BCD,
∴∠BCG=∠CGD=∠HAD,
∴AE∥CF,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:由(1)可知∠BCF=∠DCF=∠F,
∴BF=BC=AD=8,
∵AB=CD=5,
∴AF=BF﹣AB=3,
∵BF∥DE,
∴∠DCG=∠F,∠D=∠FAG,
∴△DCG∽△AFG,
∴![]() =
=![]() ,
,
∴DG=![]() AG,
AG,
∴AD=AG+DG=![]() AG=8,
AG=8,
∴AG=3,
∴AF+AG=3+3=6.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤,樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤![]() .
.
(1)若小王批发这两种水果正好花费了4400元,那么小王分别购买了多少斤樱桃和榴莲?填写下表,并列方程求解;
品种 | 批发价(元) | 购买斤数 | 小王应付的钱数(元) |
樱桃 | 32 | x | |
榴莲 | 40 |
(2)设小王购买两种水果的总花费为y元,试写出y与x之间的函数表达式.
(3)若要求所批发的榴莲的斤数不少于樱桃斤数的2倍,那么购买樱桃的数量为多少时,可使小王的总花费最少?这个最少花费是多少?